Выбор показателей надежности электроснабжения потребителей

Показатели надежности электроснабжения потребителей выбираются в соответствии с «Методическими указаниями по выбору нормативных показателей надежности технических устройств». Показатели надежности определяются для конкретных электроприемников или их групп. При этом рассматривается два состояния установки – работоспособное и неработоспособное.

Методика определяет выбор показателей, входящих в общую оценку эффективности функционирования установки. Эти показатели количественно учитывают свойства надежности СЭС, а также степень и характер влияния СЭС на выполнение установкой ее функций.

Рассмотрим факторы, влияющие на выбор номенклатуры показателей. При выборе последних учитывается характер и режимы использования установки по назначению, а именно:

· принципы ограничения длительности эксплуатации,

· временной режим использования установки,

· фактор последствий отказов.

По принципам ограничения длительности эксплуатации установки, получающие электроэнергию от СЭС, делятся на установки, эксплуатируемые в режиме ожидания, когда они эксплуатируются до достижения ими обусловленного предельного состояния, и в режиме работы, когда установки работают до отказа или до окончания выполнения требуемых функций.

По факторам временного режима использования установки делятся на эксплуатируемые в непрерывном режиме; циклическом (циклы равной длительности – циклически регулярный режим); повторно-прерывистом режиме (циклы случайной длительности – циклически нерегулярный режим).

По последствиям отказа установки делятся на подклассы в зависимости от того, какой фактор является основным при оценке последствий отказа:

· отказ независимо от длительности простоя и выполнения задания;

· выполнение или невыполнение установкой функций в заданном объеме и времени;

· вынужденный простой установки в рабочее время;

· отказ и вынужденный простой установки в рабочее время;

· выполнение установкой заданных функций в заданном объеме в произвольный момент времени.

Для характеристики надежности электроснабжения потребителей применяются следующие показатели: P (t), Q (t), T _o, T _в, λ, K _г, K _ти, K _ог.

Выбор номенклатуры показателей надежности электроснабжения осуществляется по шифрам (табл. 2.5).

Таблица 2.5

Шифры показателей надежности

Опреде-ление класса	Признак деления на под­классы	Номер и определение подкласса установки	Признак деления на группы	Номер и определение группы
Первый класс Харак-тер ре­жи­­ма исполь­зо­вания по назна­чению	Ограниче-ние про­дол­­житель­­ности эк­сплу­­а­та­ции	1. До достижения пре­­дельного со­сто­яния в режиме ожидания. 2. До достижения пре­дельного состо­яния в режиме ожидания или до отказа или до окончания выполнения тре­бу­е­мых функций в режиме работы.	Времен-ной режим ис­поль­зования по на­з­на­­чению	1. Непрерыв-ный режим 2. Циклически ре­­­гулярный ре­жим 3. Циклически не­­регулярный ре­жим
Второй класс Послед-ствия отказа	Доминиру-ющий фактор при оценке послед­ствий отказа	1. Наличие отказа неза­ви­симо от дли­тельности простоя. 2. Выполнение или невы­пол­нение ус­тановкой за­дан­ных функций в за­дан­ном объеме. 3. Вынужденный простой. 4. Наличие отказа и вы­нуж­денный про­стой. 5. Выполнение или не­вы­пол­­нение ус­тановкой фун­к­ций в заданном объеме в произвольный момент вре­мени.

Цифры шифра означают: первая цифра – номер подкласса из первого класса, вторая – номер группы из первого класса, третья – номер подкласса второго класса.

В табл. 2.6 приведены шифры установок и соответствующие им показатели надежности.

Таблица 2.6

Шифры установок и показатели надежности

Шифр установки	Показатели надежности
122, 132	P (t) или Q (t),
111, 121, 131	λ{ а, ω} или Т о
	K ти
123, 133	K г
	K ти, λ{ а, ω} или Т о
124, 134	K г, λ{ а, ω} или Т о
115, 125, 135, 215, 225, 235	K ог

В случаях, когда в соответствии с табл. 2.5 нормируемыми показателями надежности являются K _г, K _ти, K _ог, в нормативно-технической документации должны указываться показатели отдельных свойств надежности P (t), T _o, T _в, которые определяют значения коэффициентов K _г, K _ти, K _ог.

Однако критерием для сравнения показателей надежности электроснабжения должен быть показатель, приведенный в табл. 2.6.

Выбору показателей надежности должно предшествовать установление критериев отказа установки. Критерии отказа устанавливаются в следующем порядке: определяются перечень параметров установки и допускаемые пределы их изменения в соответствии с требованиями, предъявляемыми к данной установке и условиям ее эксплуатации; задается перечень технических параметров, определяющих работоспособность установки; рассчитываются величины допусков, выход за пределы которых означает отказ.

Затем по табл. 2.6 находится критерий ограничения продолжительности эксплуатации, временный режим использования, доминирующий фактор последствий отказа.

Доминирующим фактором рассматривается факт выполнения или невыполнения установкой заданной функции в заданном объеме, если использование установки связано с выполнением конкретного задания.

Факт вынужденного простоя рассматривается как доминирующий в тех случаях, когда при оценке последствий, вызванных отказом в электроснабжении, определяющую роль играет вынужденный простой установки, а величина ущерба пропорциональна длительности простоя.

Факт отказа может стать доминирующим, если наличие отказа приводит к невыполнению какой-либо конкретной задачи. Простой, вызванный отказом, не играет определяющей роли при оценке последствий.

По выбранному шифру устанавливаются нормируемые показатели надежности эксплуатации электроснабжения установки.

Пример. 2.11. Требуется выбрать показатели надежности электрического освещения производственного цеха промышленного предприятия.

Решение. Система освещения относится к установкам, которые эксплуатируются до предельного состояния, т.е. до тех пор, пока существует рассматриваемый объект – цех. В соответствии с этим согласно табл. 2.6 берется первая цифра шифра (1).

Временной режим использования электроосвещения приближенно можно считать циклически регулярным.

Доминирующими факторами при оценке последствий являются факт отказа и вынужденный простой. Таким образом, шифр установки – 124.

По табл. 2.6 определяем, что нормируемыми показателями являются коэффициент готовности и среднее время безотказной работы (или интенсивность или эквивалентные ей частота или параметр потока отказов).

2.5. Теоретические распределения наработки до отказа

Возможны два пути определения показателей надежности объектов по данным об отказах. Первый из них основан на анализе экспериментального распределения, второй – на вычислении параметров теоретического распределения наработки до отказа. Оба пути имеют достоинства и недостатки. Исторически сложилось так, что вероятностные методы исследования развивались в основном по пути использования теоретических распределений.

В качестве этих распределений могут быть использованы любые применяемые в теории вероятностей непрерывные распределения. Практически можно взять любую кривую, площадь поверхности под которой равна единице, и использовать ее в качестве кривой распределения случайной величины. Однако на практике чаще используются следующие распределения: экспоненциальное, усеченное нормальное, распределение Релея, гамма-распределение, распределение Вейбулла.

При экспоненциальном распределении наработки до отказа интенсивность отказов является постоянной величиной, т.е. 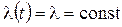. В этом случае мы имеем, так называемый пуассоновский процесс, для которого

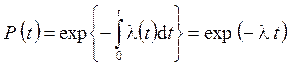, (2.38)

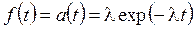, (2.39)

Если объекты характеризуются очень малыми численными значениями интенсивности отказов и, соответственно, большими значениями средней наработки на отказ, то экспоненты, получаемые по формулам (2.38), (2.39), имеют в реальном масштабе очень пологий вид. Это дает основание заменить их прямыми, касательными к экспонентам в точке t = 0. Математически это означает разложение экспоненты в ряд Тейлора и отбрасывание членов ряда, имеющих высокий порядок малости. Учитывая это, получаем упрощенные формулы для расчета показателей надежности:

P (t) = 1 – λ t, (2.38')

а (t) = λ (1 – λ t). (2.39')

Упрощенные формулы допустимо применять при λ << 1 год^-1.

Средняя наработка до отказа определится

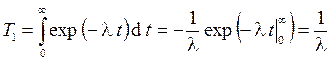. (2.40)

Графики вышеприведенных зависимостей при экспоненциальном распределении наработки до отказа приведены на рис. 2.6. Площадь под кривой Р(t) численно характеризует среднюю наработку на отказ.

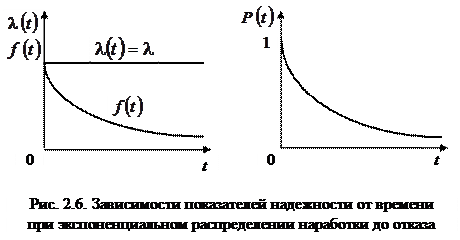Экспоненциальный закон хорошо описывает внезапные отказы, т.е. он справедлив для периода нормальной эксплуатации. Экспоненциальное распределение применяется чаще других при исследовании надежности объектов. Это объясняется рядом причин.

Во-первых, экспоненциальное распределение наработки до отказа типично для сложных объектов, состоящих из многих элементов с различными распределениями наработки до отказа.

Во-вторых, при постоянных интенсивностях отказов объектов получаются простые формулы для расчета надежности. Это связано с тем, что при 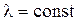вероятность безотказной работы в течение заданной наработки 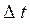не зависит от суммарной наработки.

В-третьих, при ограниченном числе экспериментальных данных трудно обнаружить значительные отклонения от гипотезы 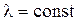даже при имеющейся возможной нестационарности 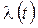. При недостаточном числе экспериментальных данных значение 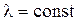принимается в качестве первого приближения.

Можно считать допустимым и оправданным применение экспоненциального закона для расчета нерезервированных систем с высокими требованиями к безотказности элементов для любой модели отказов (внезапных и постепенных), но он лишает возможности правильно прогнозировать поведение изделия при повышении его ресурса, делать правильные выводы о мероприятиях по повышению надежности системы.

Применение экспоненциального закона допустимо и оправдано при анализе и расчете надежности систем, уже обладающих высокой безотказностью, но его нельзя применять для случаев прогнозирования поведения этих систем при повышении ресурса и для оценки их надежности в пределах, выходящих за значение принятого ресурса.

Пример 2.12. Определить для трансформатора с высшим напряжением 10 кВ следующие показатели надежности для момента времени 6 месяцев: а) вероятность безотказной работы; б) вероятность отказа; в) частоту отказов; г) среднюю наработку на отказ. Интенсивность отказов трансформатора λ = 0,035 год ^–1 (см. табл. 2.4).

Решение. Р (0,5) = ехр (–0,035·0,5) = 0,9827;

Q (0,5) = 1 – ехр (–0,035·0,5) = 0,0173;

а (0,5) = λ Р (0,5) = 0,035·0,9827 = 0,03439;

Т ₀ = 1/0,035 = 28,6 лет.

Результаты расчетов показателей надежности по упрощенным формулам:

Р (0,5) = 1 – 0,035·0,5 = 0,9825;

Q (0,5) = 0,035·0,5 = 0,0175;

а (0,5) = 0,035(1 – 0,035·0,5) = 0,03438.

Плотность нормального распределения имеет колоколообразную форму, симметричную относительно среднего значения. В данном случае функция распределения записывается как

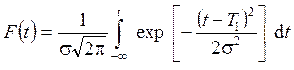, (2.41)

.

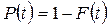Этот интеграл не вычисляется в замкнутом виде, поэтому в приложении 1 приведена табл. П.7 для этого распределения и она может использоваться для нахождения вероятностей любого нормального распределения.

Плотность нормированного нормального распределения можно представить как

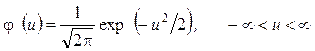, (2.42)

где 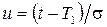. Тогда функция нормированного нормального распределения имеет вид

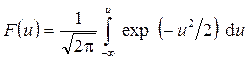. (2.43)

Для случайной величины T, распределенной по нормальному закону с математическим ожиданием T ₁ и средним квадратическим отклонением σ, выражение

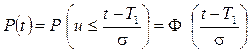(2.44)

является необходимым соотношением для использования таблицы (П7).

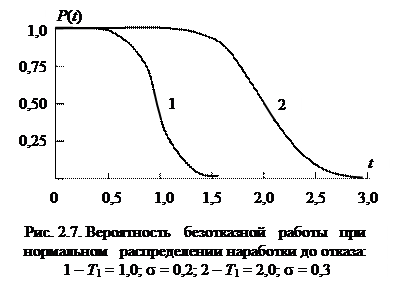
В случае нормального распределения интенсивность отказов является монотонно возрастающей функцией времени t. Это легко показать, доказав, что 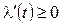для всех t. Так как

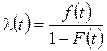, то 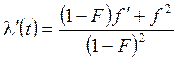. (2.45)

Вероятность безотказной работы и интенсивность отказов для некоторых нормальных распределений показаны на рис. 2.7 и 2.8 соответственно.

Пример 2.13. Элемент имеет нормальное распределение наработки до отказа с параметром Т ₁ = 20000 циклов и s = 2000 циклов. Найдите надежность элемента и интенсивность отказов при наработке, равной 19000 циклов.

Решение. Вероятность безотказной работы связана с нормированной случайной величиной u, распределенной по нормальному закону следующим соотношением:

,

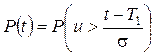тогда 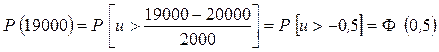. Значение функции Ф(u) находим с помощью таблицы (П.7). Имеем P (19000)=0,69146.

Значение интенсивности отказов может быть найдено с помощью соотношения

,

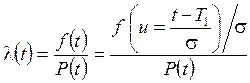где 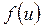определяется с помощью таблицы (П.8). В данном случае

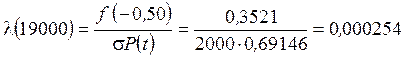отказ/цикл.

Усеченным нормальным распределением случайной величины называется распределение, получаемое из нормального при ограничении интервала возможных значений этой величины. В интервале (t ₁, t ₂ ) плотность усеченного распределения

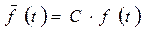, (2.46)

где 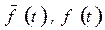- плотности усеченного и неусеченного нормальных распределений:

;

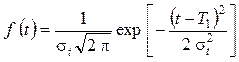С - нормирующий множитель, определяемый из условия единичной площади под кривой распределения

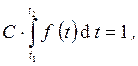откуда 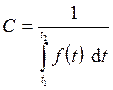; (2.47)

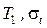- среднее значение и среднее квадратичное отклонение неусеченного распределения.

После подстановки в формулу (2.47) функции 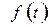с учетом обозначения 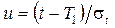, получим:

, .

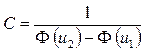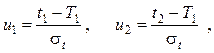
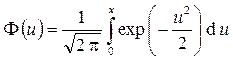Значения нормированной функции Лапласа 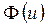приведены в таблице (П.3).

Ниже приводятся основные показатели надежности для усеченного распределения, а именно:

· вероятность безотказной работы

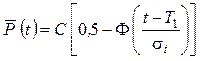; (2.48)

· интенсивность отказов

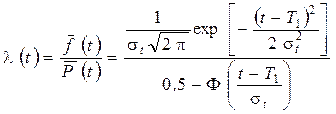. (2.49)

Практически при оценке времени безотказной работы с помощью нормального распределения может иметь место частный случай, при котором средняя наработка до отказа Т ₁ значительно больше среднего квадратического отклонения, т.е. 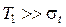. При этом

.

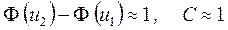Тогда основные показатели надежности при нормальном законе распределения находятся по формулам:

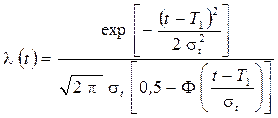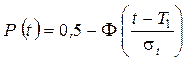; . (2.50)

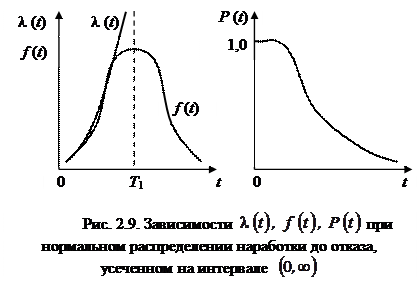Графики зависимостей 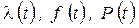при нормальном распределении наработки до отказа, усеченном на интервале 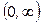, приведены на рис. 2.9.

Если способность объекта выполнять заданные функции характеризуется параметром Y с допустимыми пределами изменения 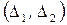, то вероятность безотказной работы объекта в течение времени t составляет

,

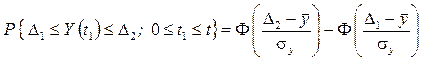где 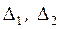- нижняя и верхняя границы поля допуска; 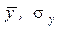- среднее значение и среднее квадратическое отклонение параметра Y.

При распределении времени возникновения отказов по логарифмически нормальномузакону плотность распределения имеет вид

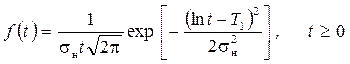, (2.51)

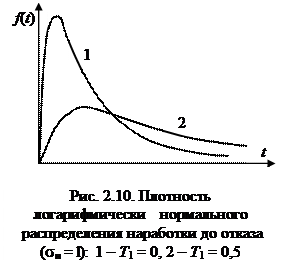где Т ₁ и s_н - параметры распределения, 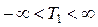и s_н > 0. Различные кривые плотности логарифмически нормального рас­пределения показаны на рис. 2.10.

Если случайная величина X определяется как x = ln T, то X имеет нормальное распределение с мате­мати­чес­ким ожиданием T ₁ и средним квадратическим отклонением s_н, т. е.

, .

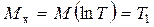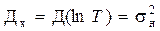Так как t = e^x, математическое ожидание логарифмически нормального распределения можно найти с помощью нормаль­ного распределения. Полагая, что

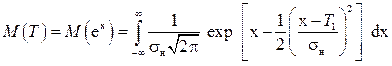(2.52)

и преобразуя экспоненту в (2.52), получаем

.

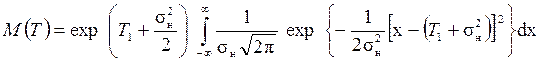Математическое ожидание логарифмически нормального распределения имеет вид

.

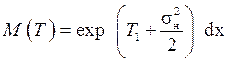Продолжая аналогичные преобразования, имеем

.

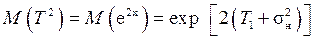Таким образом, дисперсия логарифмически нормального распре­деления имеет вид

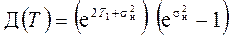. (2.53)

Функция логарифмически нормального распределения

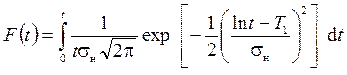, (2.54)

ее можно связать с нормированной слу­чайной величиной u, распределенной по нормальному закону, следующим образом:

. (2.55)

Вероятность безотказной работы записывается как

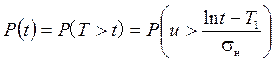, (2.56)

а интенсивность отказов имеет вид

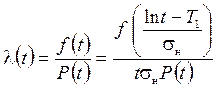, (2.57)

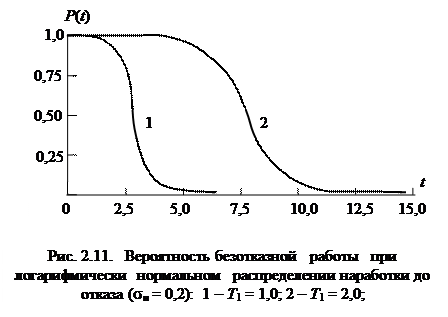
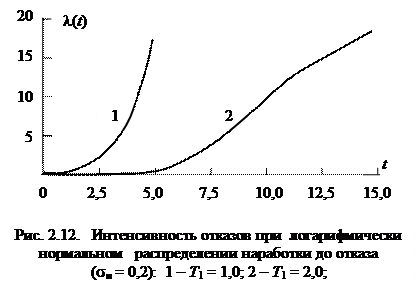
где f – плотность нормированного нормального распределения, а Т ₁ и s - соответственно математическое ожидание и среднее квадратическое отклонение натурального логарифма случайной величины T ₁, обозначающей наработку до отказа. На рис. 2.11 и 2.12 показаны графики функции соответственно вероятности без­отказной работы и интенсивности отказов для различных лога­рифмически нормальных распределений.

Пример 2.14. Наработка некоторого элемента до отказа имеет логарифмически нормальное распределение с параметрами T ₁ = 5 и s_н=1. Найдите вероятность безотказной работы элемента и интенсивность отказов при наработке, составляющей 150 часов.

Решение. Подставляя в формулу (2.56) численные значения T ₁ , s_н и t, получаем

.

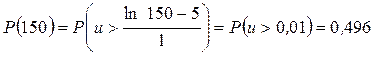Используя выражение (2.57) для интенсивности отказов, имеем

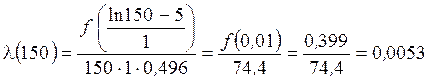отказа в час.

Таким образом, значения функции логарифмически нормаль­ного распределения легко вычислить, используя таблицы для нормированного нормального распределения.

При распределении времени возникновения отказов по закону Релея плотность распределения f (t) задается выражением

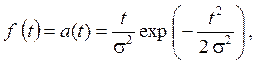(2.58)

где s - параметр распределения Релея. Тогда вероятность безотказной работы, интенсивность отказов и средняя наработка до отказа выражаются следующими формулами:

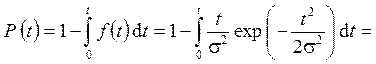
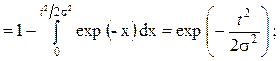(2.59)

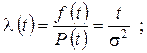(2.60)

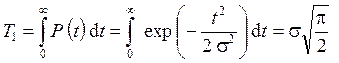. (2.61)

При вычислении использован табличный интеграл

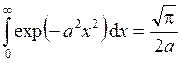, при а > 0.

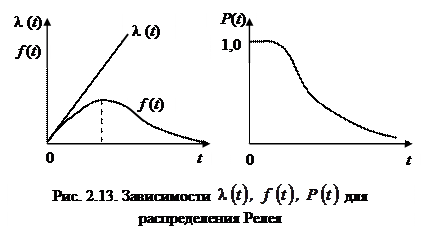Зависимости ос­нов­ных количественных характеристик на­деж­но­сти для распределения Релея приведены на рис. 2.13. Из формулы для интенсивности отказов видно, что эта ин­тен­сив­ность растет линейно с те­чением времени. Поэ­то­му распределение Ре­лея применимо для описания характеристик надежности объектов с явно выраженным эффектом старения, например электровакуумных приборов.

Гамма - распределение используется при оценке надежности объектов в начальный период эксплуатации, при исследовании надежности электромеханических объектов, высоконадежной электронной аппаратуры с интенсивностью отказов, уменьшающейся во времени. Оно описывает также распределение времени отказов объектов, резервированных способом замещения, если наработка на отказ основного и резервного объектов следует экспоненциальному закону.

Плотность гамма-распределения задается выражением

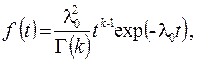(2.62)

где Г(k) = (k– 1)! - гамма-функция, определяемая по формуле

.

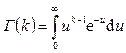В теории надежности гамма – распределение используется при целом k. При k > 1 гамма-распределение является распределением суммы k независимых случайных величин, каждая из которых имеет экспоненциальное распределение с параметром 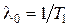. Для такого распределения

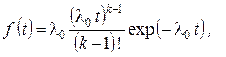(2.63)

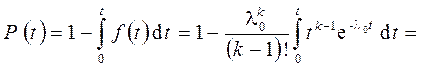
(2.64)

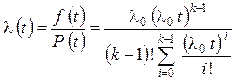, (2.65)

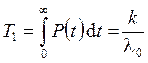. (2.66)

Дисперсия времени безотказной работы 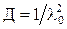. Математическое ожидание числа отказов n на интервале времени, равном t, составит n = λ₀ t.

Параметр формы k характеризует асимметрию и эксцесс гамма – распределения. В зависимости от его величины существенно изменяется вид основных количественных характеристик надежности. Зависимости f (t), l(t) и P (t) приведены на рис. 2.14, из которого видно, что при k = 1 гамма–распределение превращается в экспоненциальное распределение. При k >1 интенсивность отказов возрастает, а при k < 1 – убывает.

Пример 2.16. Наработка некоторого элемента до отказа имеет гамма-распределение с параметрами k = 3 и l₀ = 0,05. Определите вероятность безотказной работы элемента и интенсивность отказов при наработке, равной 24 часам.

Решение. Используя формулу (2.64), определяем

.

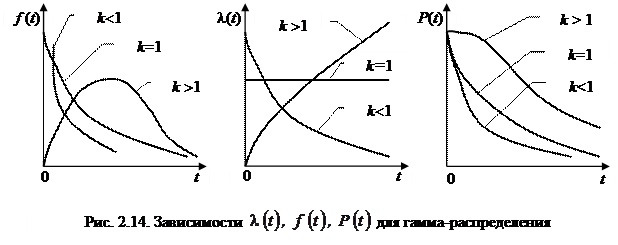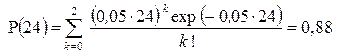С помощью формулы (2.63) вычисляем

.

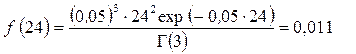По формулам (2.65), (2.66) получаем

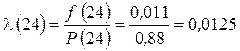отказа в 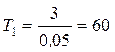ч,

ч.

При исследовании характеристик надежности полупроводниковых приборов, при ускоренных испытаниях объектов в форсированных режимах, при анализе надежности объектов в период приработки используется распределение Вейбулла. Модель надежности Вейбулла, называемая также моделью Вейбулла-Гнеденко, была предложена шведским ученым В. Вейбуллом в качестве модели прочности материалов, а затем обоснована математически советским ученым Б.В.Гнеденко. Плотность распределения наработки до отказа в этом случае определяется выражением

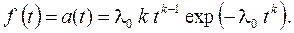(2.67)

Параметр 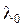задает масштаб кривой по оси абсцисс, а параметр k – асимметрию и эксцесс распределения. Ориентировочно значение k = 0,2…0,4 для электронных устройств с убывающей функцией интенсивности отказов и k =1,2…1,4 для механических устройств с возрастающей функцией интенсивности отказов.

Для распределения Вейбулла основные количественные характеристики надежности выражаются следующими формулами:

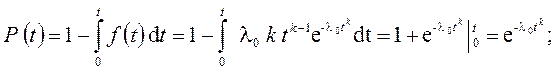(2.68)

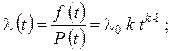(2.69)

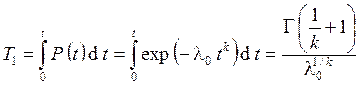, (2.70)

где Г- гамма-функция.

Дисперсия времени безотказной работы

.

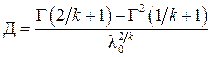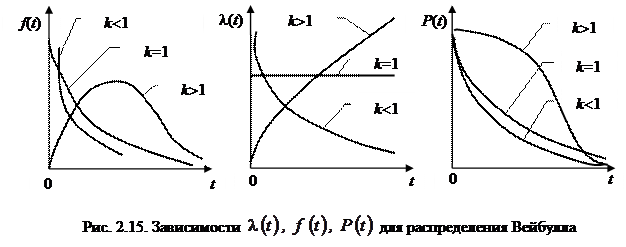
Зависимости основных количественных характеристик надежности от времени приведены на рис. 2.15. Из рисунка видно, что при k = 1 распределение Вейбулла превращается в экспоненциальное распределение. При k >1 интенсивность отказов начинается с нуля и с течением времени возрастает. При k <1 интенсивность отказов начинается с + ¥ и в области больших t стремится к нулю. При соответствующем подборе параметра k можно с помощью закона Вейбулла описывать надежность и стареющих элементов, у которых λ₀(t) возрастает, и надежность элементов, имеющих скрытые дефекты, у которых λ₀(t) убывает с течением времени. Закон Вейбулла очень удобен для вычислений, но связан с эмпирическим подбором параметров λ₀ и k для имеющейся зависимости λ₀(t).

Пример 2.17. Наработка некоторого элемента до отказа имеет распределение Вейбулла с параметрами k = 4, в интервале времен от 1000 до 2000 ч. Найти вероятность безотказной работы элемента и интенсивность отказов при наработке, равной 1500 ч.

Решение. Подставляя заданные значения в формулу (2.68), получаем

.

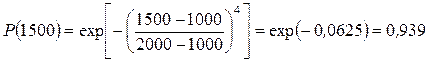С помощью формулы (2.69) находим искомую интенсивность отказов:

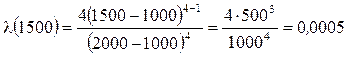отказ/ч.

Пример 2.18. Время безотказной работы устройства подчиняется закону Вейбулла с параметрами k = 1,5 λ₀ = 10^–4 1/ч, время работы t = 100 ч. Требуется вычислить количественные характеристики надежности устройства.

Решение. Определим вероятность безотказной работы по формуле (2.68)

Р(100) = exp(–10^–4·100^1,5) = 0,9.

Частота отказов определяется по формуле (2.67)

а (100) = 10^–4·1,5·100^0,5·0,9 = 1,35·10^–3 1/ч.

Интенсивность отказов определяем по формуле

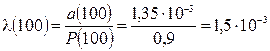1/ч.

Вычислим среднюю наработку до первого отказа по формуле (2.70). Вычислим вначале значение гамма-функции. В нашем случае х = (1/ k)+1 = (1/1,5)+1 = 1,67, тогда Г(х) = 0,9033. Подставляя значение Г(х) и параметры распределения λ и k в выражение для Т₁, получим

Т₁ = 0,9033/(10^–4)^1/1,5 = 418 ч.

Пример 2.19. Определить вероятность безотказной работы устройства для экспоненциальной модели и модели Вейбулла через 10⁵ ч работы при условии, что Р = 0,99 за время работы t = 1000 ч.

Решение. В случае экспоненциальной модели интенсивность отказов λ = 10^–5 1/ч.

В случае модели Вейбулла при k = 0,5 λ₀ = –ln P (t)/ t^k =0,000316. Следовательно, через 10⁵ ч работы вероятность безотказной работы, прогнозируемой по экспоненциальной модели, равна Р _э = exp(–10^-5·10⁵) = 0,37. Прогноз по модели Вейбулла Р _в = exp(–0,000316·10^2,5) = 0,905. Следовательно, выбор правильной модели надежности не безразличен для практики.

Выбор модели надежности – сложная научно-техническая проблема. Она может быть удовлетворительно решена стандартными методами математической статистики, если имеется большой статистический материал об отказах исследуемых объектов. В случае приближенных оценок часто выбирается экспоненциальная модель как наиболее удобная с точки зрения аналитических преобразований. Экспоненциальную модель рекомендуется применить при выполнении расчетов надежности в случае отсутствия других исходных данных для расчета, кроме интенсивности отказов. В случае наличия более полных исходных данных целесообразно пользоваться другой, более точной моделью, например моделью Вейбулла.

На этом заканчивается нахождение распределений наработки до отказа и соответствующих им вероятностей безотказной ра­боты и интенсивностей отказов.