Достаточное условие экстремума. Для формулировки теоремы, выражающей достаточное условие экстремума с помощью первой производной, нам понадобится одно предварительное понятие

Для формулировки теоремы, выражающей достаточное условие экстремума с помощью первой производной, нам понадобится одно предварительное понятие.

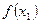
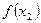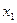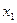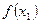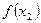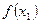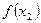Говорят, что функция у = меняет знак при переходе через точку х = х ₀, если < 0 для любых и х ₂из некоторой ок­рестности этой точки, удовлетворяющих неравенствам < х ₀ < х ₂ знак меняется с плюса на минус, если > 0, а < 0; знак меняет­ся с минуса на плюс, если < 0, > 0.

Формулируя теоремы 4.1 и 4.2, будем предполагать, что функция у= дифференцируема в некоторой окрестности точки х ₀.