Экстремум функции. Необходимое условие экстремума

Рассмотрим функцию, у = областью определения которой является промежуток (а, b)

Если можно указать такую 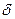- окрестность точки 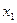, принадле­жащую промежутку (а, b ), то для всех 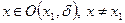, выполняет­ся неравенство

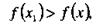(8)

то у 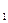= 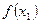называют максимумом функции у = . Мак­симум функции у = обозначается через .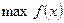

Если можно указать такую 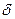-окрестность точки х ₂, принадле­жащую промежутку (а, b), что для всех 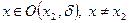, выполняет­ся неравенство

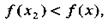(9)

то у 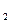= 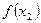называют минимумом функции у = . Минимум функции у = обозначим через .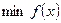

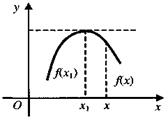
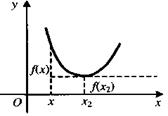
Другими словами, максимумом (минимумом) функции у = называют такое ее значение, которое больше (меньше) всех других значений, принимаемых в точках, достаточно близких к данной и от­личных от нее.

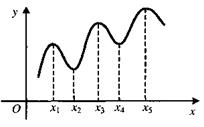Отметим, что максимум и минимум функции имеют локальный характер (это наибольшее и наименьшее значение функции в доста­точно малой окрестности соответствующей точки); отдельные мини­мумы некоторой функции могут оказаться больше максимумов той же функции.

Максимум и минимум функции называются экстремумом. Зна­чение аргумента, при котором достигается экстремум, называется точ­кой экстремума. Необходимое условие экстремума выражается сле­дующей теоремой.