Основные понятия. Пусть имеются два алфавита: – кодируемый и – кодирующий

Глава 3. ЭЛЕМЕНТЫ ТЕОРИИ КОДИРОВАНИЯ

Пусть имеются два алфавита: 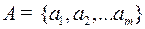– кодируемый и 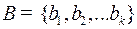– кодирующий.

Символами алфавитов могут быть буквы, цифры или иные знаки, например, точки и тире. Не умаляя общности, символы алфавитов будем называть буквами.

Словом в алфавите 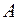называется любая последовательность букв этого алфавита: 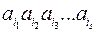. Словом в алфавите 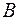называется любая последовательность букв этого алфавита 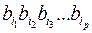. Множество слов алфавитов 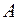и 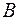обозначим 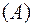ɱ и ɱ .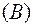

Кодированием называется отображение 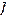множества ɱ 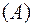на множество ɱ 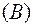. Кодом слова 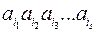называется слово 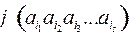, принадлежащее ɱ .

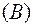Мы будем рассматривать алфавитное (буквенное) кодирование. При алфавитном кодировании задается код каждой буквы алфавита 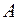,который называется кодовым словом:

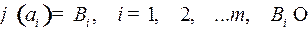ɱ 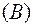, , 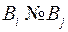если .

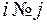Тогда кодом слова 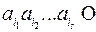ɱ 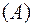будет последовательность кодовых слов .

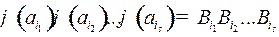Набор кодовых слов 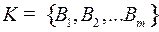называется кодом.

Код называется взаимно-однозначным или однозначно декодируемым, если коды любых двух различных слов будут различны, иными словами, код будет взаимно-однозначным, если 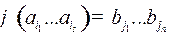можно однозначным образом разбить на кодовые слова, то есть представить 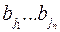в виде .

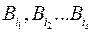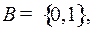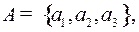
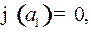
Пример 1. Алфавит алфавит 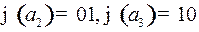, то есть .

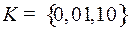Пусть 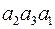– слово в алфавите 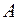, 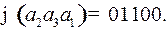По этому коду исходное слово восстанавливается однозначно: первым кодовым словом может быть только 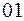(0 не может быть кодовым словом, так как нет кодового слова 1, или 11, или 110), тогда вторым кодовым словом может быть только 10 и, наконец, 0 – код буквы .

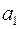Рассмотрим в алфавите 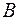слово 010, его можно разбить на кодовые слова двумя способами как 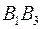или 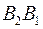, то есть коды двух разных слов 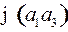и 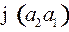совпали. Кодирование, заданное таким набором кодовых слов, хотя сами кодовые слова разные, не является однозначным.