1. Пусть в графе 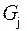 нет ориентированных циклов через вершину
нет ориентированных циклов через вершину 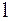 , покажем, что кодирование взаимно-однозначное.
, покажем, что кодирование взаимно-однозначное.
Предположим противное: существуют слова, которые неоднозначно декодируются, то есть неоднозначно разбиваются на кодовые слова. Среди всех неоднозначно декодируемых слов выберем самое короткое слово 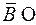 ɱ
ɱ 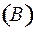 и рассмотрим два разных разбиения его на кодовые слова.
и рассмотрим два разных разбиения его на кодовые слова.
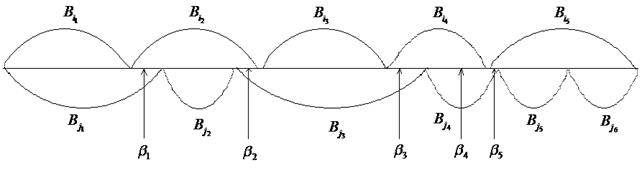
Рис. 44
На рис. 44 сверху показано одно разбиение слова 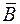 на кодовые слова, снизу другое. Точки сечений не совпадают, так как
на кодовые слова, снизу другое. Точки сечений не совпадают, так как 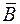 самое короткое слово,
самое короткое слово, 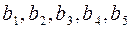 – собственные префиксы и суффиксы кодовых слов. Тогда в графе
– собственные префиксы и суффиксы кодовых слов. Тогда в графе 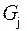 существует орцикл через вершину
существует орцикл через вершину 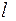 .
.
Действительно, из 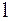 идет дуга в
идет дуга в 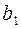 , так как существует кодовое слово
, так как существует кодовое слово 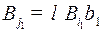 , из
, из 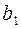 в
в 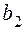
 идет дуга, так как существует кодовое слово
идет дуга, так как существует кодовое слово 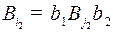 , из
, из 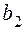 идет дуга в
идет дуга в 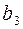 , так как существует кодовое слово
, так как существует кодовое слово 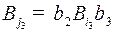 , из
, из 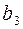 в
в 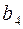 идет дуга, так как кодовое слово
идет дуга, так как кодовое слово 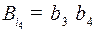 (в этом случае
(в этом случае 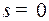 ), из
), из 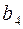 в
в 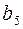 идет дуга: слово
идет дуга: слово 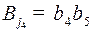 , наконец, из
, наконец, из 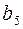 в
в 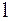 идет дуга, так как существует слово
идет дуга, так как существует слово 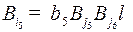 . Найдя орцикл
. Найдя орцикл 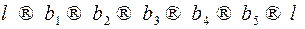 , мы пришли к противоречию, следовательно, предположение о неоднозначности декодирования неверно.
, мы пришли к противоречию, следовательно, предположение о неоднозначности декодирования неверно.
2. Пусть кодирование взаимно-однозначное, покажем, что в 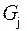 нет орциклов через вершину
нет орциклов через вершину  . Доказательство проведем от противного.
. Доказательство проведем от противного.
а) Рассмотрим самый короткий цикл через вершину 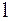 – это петля (рис. 45).
– это петля (рис. 45).
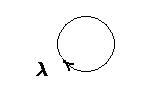 Рис. 45 Рис. 45 | Но если из 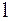 в в 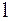 идет дуга, то существуют кодовые слова идет дуга, то существуют кодовые слова 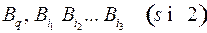 такие, что такие, что 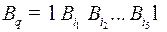 , тогда , тогда 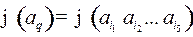 –декодирование неоднозначное. –декодирование неоднозначное. |
б) Пусть орцикл проходит через две вершины (рис. 46).
 Рис. 46 Рис. 46 | Рассмотрим сообщение вдоль этого цикла: 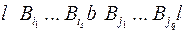 которое допускает два разных разбиения на кодовые слова которое допускает два разных разбиения на кодовые слова 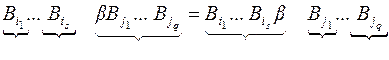 , где , где 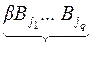 и и 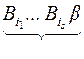 – разные кодовые слова. – разные кодовые слова. |
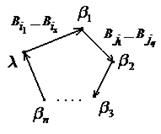 Рис. 47 Рис. 47 | в) Рассмотрим произвольный орцикл через вершину 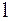 , тем не менее самый короткий, без повторяющихся вершин (рис. 47). Различные разбиения на кодовые слова связаны с тем, куда мы будем относить вершины , тем не менее самый короткий, без повторяющихся вершин (рис. 47). Различные разбиения на кодовые слова связаны с тем, куда мы будем относить вершины 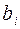 . Одна расшифровка будет такая: . Одна расшифровка будет такая: 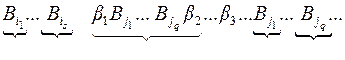 |
Другая расшифровка:
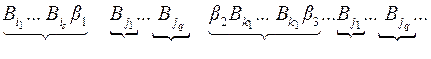 и вновь имеем неоднозначное декодирование.
и вновь имеем неоднозначное декодирование.
Пример 2. Рассмотрим код 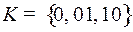 из примера 1, он был неоднозначным, следовательно, должен существовать цикл через вершину
из примера 1, он был неоднозначным, следовательно, должен существовать цикл через вершину 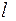 . Множество
. Множество 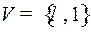 , из
, из 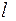 идет дуга в 1, так как существуют кодовые слова 0 и 01 такие, что
идет дуга в 1, так как существуют кодовые слова 0 и 01 такие, что 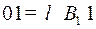 , из 1 идет дуга в
, из 1 идет дуга в 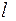 , так как существует слово
, так как существует слово 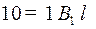 .
.
Пример 3. Выяснить, является ли взаимно-однозначным код
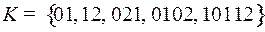 .
.
Здесь множество 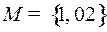 . Для того чтобы дуга выходила из вершины
. Для того чтобы дуга выходила из вершины 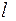 , нужно чтобы существовало кодовое слово, которое начинается с другого кодового слова, а чтобы входила в вершину
, нужно чтобы существовало кодовое слово, которое начинается с другого кодового слова, а чтобы входила в вершину 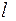 , нужно существование кодового слова, оканчивающегося на другое кодовое слово.
, нужно существование кодового слова, оканчивающегося на другое кодовое слово.
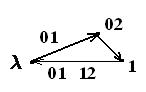 Рис. 48 Рис. 48 | В нашем случае существует цикл (рис. 48) и именно сообщение вдоль этого цикла допускает различное разбиение на кодовые слова: 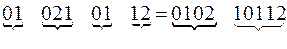 . . |
Рассмотрим простые типы взаимно-однозначных кодов.
1. Равномерный код, это код, в котором длины всех кодовых слов равны. Тогда сообщение единственным образом разбивается на куски одинаковой длины.
2. Префиксный код. Код называется префиксным, если ни одно кодовое слово не является началом другого кодового слова. В этом случае нет дуги, выходящей из вершины 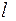 , следовательно, нет цикла через вершину
, следовательно, нет цикла через вершину 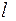 . Разбиение на кодовые слова начинается с начала сообщения: отрезаем первое кодовое, затем следующее и так далее.
. Разбиение на кодовые слова начинается с начала сообщения: отрезаем первое кодовое, затем следующее и так далее.
Префиксный код употребляется чаще других, во-первых, не надо выяснять его однозначность, во-вторых, его легко строить. Префиксный код можно строить с помощью корневого дерева, которое применительно к коду называют кодовым, где кодовым словам соответствуют только висячие (концевые) вершины.
Пусть алфавит 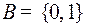 , тогда из каждой вершины корневого дерева могут выходить только две дуги, левая дуга соответствует 0, правая 1. К каждой висячей вершине корневого дерева ведет от корня единственный путь, ему и соответствует кодовое слово. Поэтому чтобы построить префиксный код для алфавита
, тогда из каждой вершины корневого дерева могут выходить только две дуги, левая дуга соответствует 0, правая 1. К каждой висячей вершине корневого дерева ведет от корня единственный путь, ему и соответствует кодовое слово. Поэтому чтобы построить префиксный код для алфавита 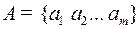 , надо построить корневое дерево, в котором будет
, надо построить корневое дерево, в котором будет 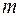 висячих вершин.
висячих вершин.
Пример 4. Пусть алфавит 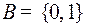 ,
, 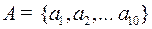 . Построим, например, корневое дерево, показанное на рис. 49
. Построим, например, корневое дерево, показанное на рис. 49
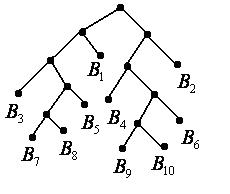 Рис. 49 Рис. 49 | 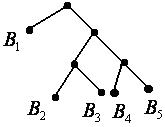 Рис. 50 Рис. 50 |
Этому дереву соответствует следующий набор кодовых слов:
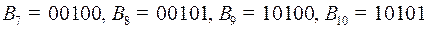 .
.
Можно построить код с заданным набором длин кодовых слов.
Пример 5. Построить двоичный префиксный код (то есть алфавит 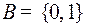 ) с набором длин кодовых
) с набором длин кодовых 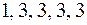 . Такому коду соответствует дерево, приведенное на рис. 50, а сам код задается кодовыми словами
. Такому коду соответствует дерево, приведенное на рис. 50, а сам код задается кодовыми словами 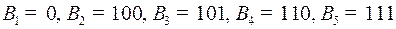 .
.
3. Суффиксный код. Код называется суффиксным, если ни одно кодовое слово не является концом другого кодового слова. Декодирование начинается с конца сообщения: отрезается последнее кодовое слово, затем предпоследнее и так далее.
 2015-05-20
2015-05-20 2261
2261








