Асимптоты

По виду уравнений относительно выбранной декартовой систе­мы координат различают асимптоты вертикальные (параллельные оси Оу) и наклонные (пересекающие ось Оу).

Переходим к определениям и рассмотрению необходимых и достаточных условий, при которых график данной функции имеет асимптоты.

Прямая х = а называется вертикальной асимптотой графика функции у = . если хотя бы одно из предельных значений 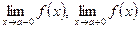является бесконечным.

Предположим, что функция у = определена при сколь угод­но больших (по модулю) значениях аргумента; для определенности будем рассматривать положительные значения аргумента.

Прямая

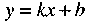(14)

называется наклонной асимптотой графика функции у = , если эта функция представима в виде

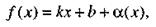(15)

где

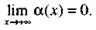(16)

Покажем, что график функции у = имеет при 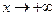на­клонную асимптоту (14) тогда и только тогда, когда существуют два конечных предела

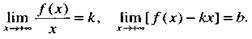(17)

т. е. существуют предельные значения (12.20).

Пусть график функции у = имеет асимптоту, определяемую уравнением (14), тогда справедливы равенства (15) и (16). Следовательно,

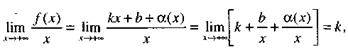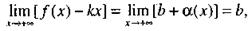т. е. существуют предельные значения (17)