Пусть заданы кодируемый алфавит 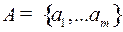 и кодирующий алфавит
и кодирующий алфавит 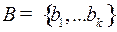 . Взаимно-однозначное кодирование
. Взаимно-однозначное кодирование 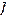 задано набором кодовых слов
задано набором кодовых слов 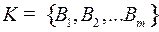 с длинами
с длинами 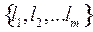 . Тогда выполняется неравенство
. Тогда выполняется неравенство 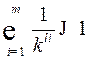 , где
, где  – количество букв в алфавите
– количество букв в алфавите  ,
, 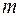 – мощность алфавита
– мощность алфавита 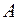 .
.
Доказательство. Обозначим 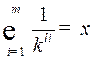 и рассмотрим
и рассмотрим 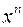 , где
, где 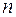 – произвольное натуральное число.
– произвольное натуральное число.
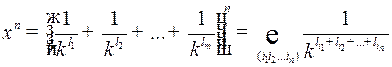 (1)
(1)
сумма берется по всевозможным упорядоченным наборам 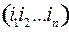 , каждое
, каждое 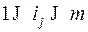 , слагаемых будет
, слагаемых будет 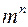 . Для пояснения такой формы записи приведем пример.
. Для пояснения такой формы записи приведем пример.
Пример 6. Рассмотрим 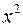 , где
, где 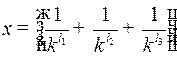 .
.
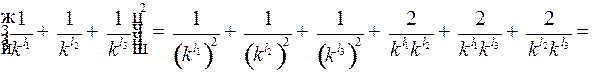
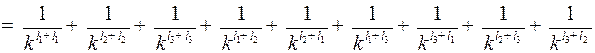 .
.
Обозначим 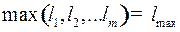 и, приведя подобные в равенстве (1), получим
и, приведя подобные в равенстве (1), получим
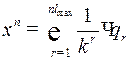 , (2)
, (2)
где 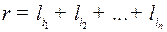 ,
, 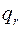 – число наборов
– число наборов 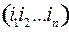 на которых
на которых 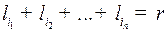 . Если для какого-то
. Если для какого-то 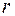 не будет ни одного набора
не будет ни одного набора 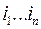 , на котором
, на котором 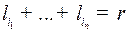 , соответствующее
, соответствующее 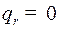 .
.
Оценим 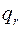 . Набору
. Набору 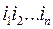 соответствует единственное слово
соответствует единственное слово 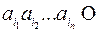 ɱ
ɱ 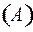 . Так как упорядоченные наборы
. Так как упорядоченные наборы 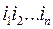 различны, то слова
различны, то слова 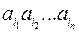 разные, кодирование
разные, кодирование 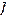 взаимно-однозначное, их коды
взаимно-однозначное, их коды 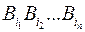 – слова в множестве ɱ
– слова в множестве ɱ 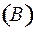 также различны. Длина слова
также различны. Длина слова 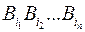 равна
равна 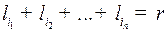 .
.
Таким образом, 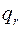 – число слов длины
– число слов длины 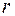 в алфавите
в алфавите 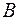 , которые являются кодами слов длины
, которые являются кодами слов длины 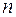 в алфавите
в алфавите 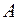 . Всех слов длины
. Всех слов длины 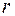 в алфавите
в алфавите 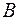
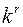 , поэтому
, поэтому 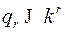 ,
,
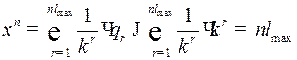 .
.
Тогда 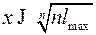 . Неравенство выполняется для любого
. Неравенство выполняется для любого 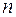 , можно перейти к пределу при
, можно перейти к пределу при 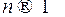 .
.
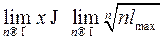 ,
,
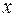 от
от 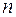 не зависит, поэтому
не зависит, поэтому 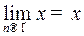 ,
, 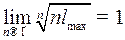 , следовательно,
, следовательно, 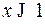 . Отсюда
. Отсюда 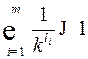 .
.
 2015-05-20
2015-05-20 3380
3380








