Для взаимного-однозначного кода выполняется неравенство Макмиллана
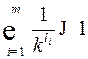 . (3)
. (3)
Пусть имеется 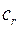 кодовых слов длины
кодовых слов длины 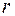 и
и 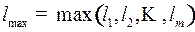 , тогда неравенство (3) можно переписать в виде (4)
, тогда неравенство (3) можно переписать в виде (4)
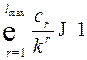 . (4)
. (4)
Для любого 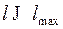 также будет справедливо
также будет справедливо
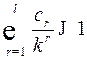 . (5)
. (5)
Умножим обе части неравенства на 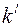 ,
,
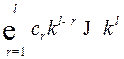 . (6)
. (6)
Перепишем это неравенство в виде:
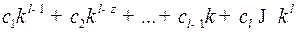 . (7)
. (7)
Откуда получим оценку для 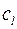 – числа слов длины
– числа слов длины 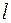 в исходном коде:
в исходном коде: 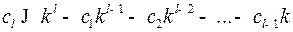 .
.
Докажем, что можно построить префиксный код, в котором кодовых слов длины 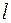 также будет
также будет 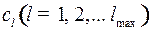 .
.
Доказательство проведем по индукции по 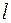 .
.
При 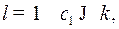 где
где  – число букв в алфавите
– число букв в алфавите 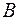 , следовательно, для префиксного кода можно выбрать
, следовательно, для префиксного кода можно выбрать 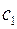 однобуквенных кодовых слов.
однобуквенных кодовых слов.
При 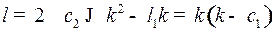 .
.
Пусть 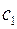 буква выбрана как однобуквенное кодовое слово, тогда для построения двухбуквенного кодового слова, обладающего свойством префикса, у первой буквы остается
буква выбрана как однобуквенное кодовое слово, тогда для построения двухбуквенного кодового слова, обладающего свойством префикса, у первой буквы остается 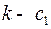 возможность, у второй буквы
возможность, у второй буквы  возможностей, то есть всего
возможностей, то есть всего 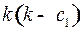 возможностей, а
возможностей, а 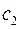 , число двухбуквенных кодовых слов в исходном коде, не превосходит этого числа.
, число двухбуквенных кодовых слов в исходном коде, не превосходит этого числа.
Пусть выбраны 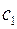 кодовое слово длины 1,
кодовое слово длины 1, 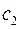 слова длины два, и так далее вплоть до
слова длины два, и так далее вплоть до 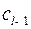 слова длины
слова длины 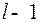 , обладающих свойством префикса.
, обладающих свойством префикса.
Покажем, что можно выбрать 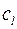 кодовых слов длины
кодовых слов длины 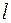 , также обладающих свойством префикса.
, также обладающих свойством префикса.
В алфавите B слов длины 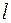 и
и 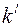 . Найдем количество запрещенных слов, начинающихся с уже выбранных кодовых слов. Если какая-то буква выбрана в качестве однобуквенного кодового слова, то запрещены все слова длины
. Найдем количество запрещенных слов, начинающихся с уже выбранных кодовых слов. Если какая-то буква выбрана в качестве однобуквенного кодового слова, то запрещены все слова длины 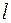 , начинающиеся с этой буквы, таких слов
, начинающиеся с этой буквы, таких слов 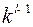 .
.
Учитывая, что однобуквенных кодовых слов 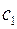 , запрещено
, запрещено 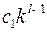 слово. Запрещены все слова длины
слово. Запрещены все слова длины 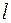 , начинающиеся с
, начинающиеся с 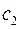 выбранных двухбуквенных слов, их
выбранных двухбуквенных слов, их 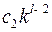 .
.
Таким образом, число возможностей для выбора кодовых слов длины 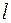 , обладающих свойством префикса равно
, обладающих свойством префикса равно
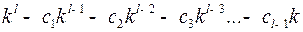 , а
, а 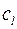 – число слов длины
– число слов длины 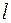 в исходном алфавите не превосходит этого числа. Следовательно, можно построить префиксный код с тем же набором длин кодовых слов, как в исходном взаимно-однозначном коде
в исходном алфавите не превосходит этого числа. Следовательно, можно построить префиксный код с тем же набором длин кодовых слов, как в исходном взаимно-однозначном коде 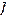 .
.
 2015-05-20
2015-05-20 650
650








