Упорядоченность вероятностей кодового дерева по ярусам

Пусть даны алфавит 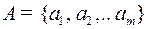с набором вероятностей 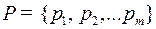, алфавит 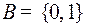, оптимальный префиксный код 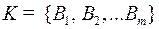, где 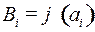, длина кодового слов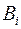а равна .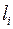

Тогда

а) если 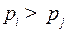то ;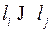

б) если 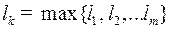и кодовое слово 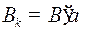, где 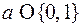, то существует кодовое слово 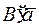, входящее в 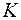, то есть кодовые слова максимальной длины в оптимальный двоичный префиксный код входят попарно.

Замечание. Код называется 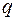-ичным, если кодирующий алфавит 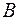содержит 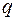символов.