Оптимальный код

В русском алфавите 32 буквы, е и ё можно считать за одну букву, предположим их надо закодировать равномерным кодом в алфавите 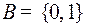. Тогда длина каждого кодового слова должна быть равна 5, любое сообщение становится длиннее в 5 раз. С другой стороны, такие буквы как щ; ч; ы; ъ; ь и так далее встречаются редко, их можно было бы закодировать более длинными кодовыми словами, а встречающиеся часто – более короткими. Так возникает идея оптимальных кодов, которая связана с частотной (вероятностной) характеристикой букв кодируемого алфавита.

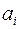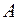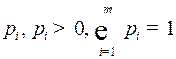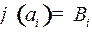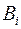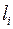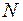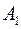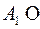Каждая буква кодируемого алфавита обладает своей частотой (вероятностью) использования в языке, обозначим ее . Пусть задано алфавитное кодирование: , длина равна . Посмотрим, как меняется при кодировании длина слова , ɱ 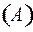, то есть найдем длину слова .

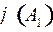Буква 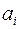входит в слово 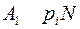раз, при кодировании она даст длину 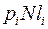, следовательно, длина слова 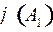будет равна

.

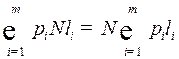Определение. Ценой кодирования называется число 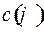, где

.

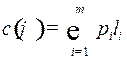Цена кодирования показывает, во сколько раз увеличивается длина любого слова при кодировании, и является средней длиной кодового слова (математическим ожиданием кодового слова).

При фиксированных алфавитах 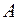и 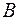рассмотрим множество 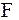взаимно-однозначных кодов 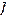, цена кодирования каждого .

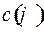Найдем 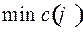на множестве 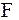, он очевидно, будет характеристикой кодируемого алфавита :

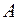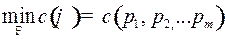. (8)

Определение. Код 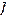, такой что 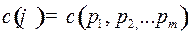, называется оптимальным кодом или кодом с минимальной избыточностью.

Пусть 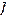– оптимальный код, заданный набором кодовых слов 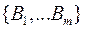с длинами 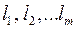. Можно построить префиксный код (по теореме о существовании префиксного кода) с тем же набором длин кодовых слов, следовательно, с той же ценой кодирования.

Замечание. Среди оптимальных кодов всегда есть префиксный код.

Пример 7. Пусть даны алфавиты 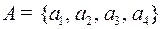с вероятностям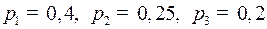и и 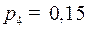и кодирующий алфавит .

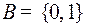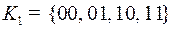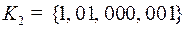Рассмотрим два кода и . Код 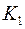– равномерный, 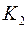– префиксный, оба однозначно декодируемые. Найдем для каждого цену кодирования.

.

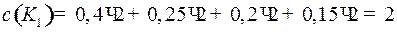
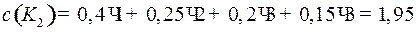Рассмотрим свойства оптимальных префиксных кодов.