2015-05-20
855
|
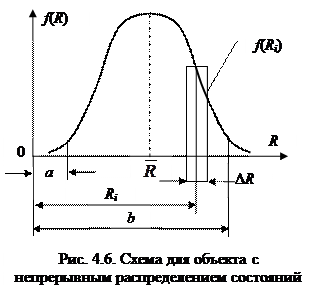
Если в качестве объекта рассматривать резистор, сопротивление которого принимает ряд случайных значений в интервале от а до b (непрерывное распределение состояний, рис. 4.6), то непрерывное распределение можно заменить дискретным. Для этого область изменения сопротивления резистора разбивается на n одинаковых интервалов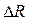 
. Тогда энтропия объекта
,
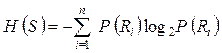где Р (Ri) - вероятность сопротивления резистора в интервале со средним значением Ri. С учетом плотности распределения f (Ri )
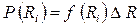
и
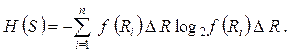(4.27)
Раскрывая логарифм произведения, приведем последнее выражение к виду
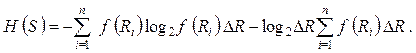
Перейдя к пределу при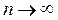 
, найдем выражение для энтропии объекта с непрерывным распределением параметров:
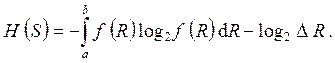(4.28)
При выводе формулы (4.28) учитывалось следующее, вытекающее из определения плотности вероятности условие:
.
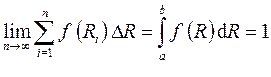Принципиальной особенностью энтропии объекта с непрерывным распределением состояний является ее зависимость от шага квантования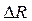 
. Выбор шага квантования обусловлен требуемой точностью при аппроксимации непрерывного распределения ступенчатым (дискретным), но само существование шага квантования связано с физической сущностью непрерывного процесса.
Величину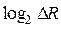 
в равенстве (4.28) можно рассматривать как начало отсчета энтропии; для многих задач оно оказывается несущественным. В общем случае объект с непрерывным распределением состояний характеризуется параметром х, изменяющимся в пределах 
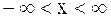, тогда
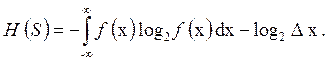(4.29)
Последнее равенство можно записать через математическое ожидание Mxслучайной величины
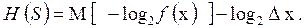(4.30)
|
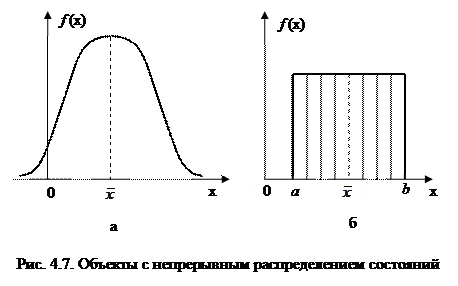
Пример 4.3. Определим энтропию объекта, состояния которого (значения х) подчиняются закону нормального распределения (рис. 4.7, а). С учетом плотности распределения х, заданной выражением
,
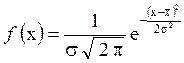энтропия (4.30) принимает следующий вид:
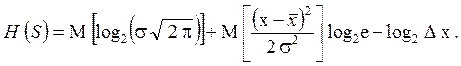
Так как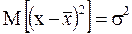 
, то
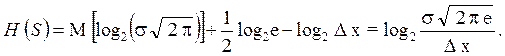(4.31)
Отметим, что энтропия в данном случае не зависит от среднего значения параметра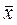 
и определяется отношением 
.
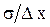Пример 4.4. Определим энтропию объекта, состояния которого равновероятны на участке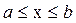 
(рис. 4.7,б). В этом случае
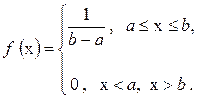
Из формулы (4.29) получаем:
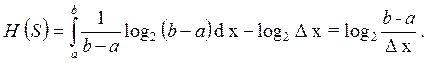(4.32)
