Коэффициент Корреляции

Корреляционный анализ

Технологических параметров

Самара, 2008

Составители: Б.Н. Березков, А.В. Архипов

УДК

Корреляционный анализ технологических параметров: Метод. указания к лаб. раб./ Сост. Б.Н.Березков, А.В. Архипов. - Самара: Изд-во Самар.гос.аэрокосм. ун-та,2008.

Цель работы: применение корреляционных зависимостей для установления связей между технологическими параметрами.

Общие положения

При изучении зависимости между двумя величинами, каждая из которых подвергается случайному рассеиванию (неконтролируемому разбросу), применяется методы корреляционного анализа. Корреляционный анализ изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру зависимости между рассматриваемыми величинами. Сопоставляя каждому значению одной величины, скажем x, среднее из соответствующих значений другой величины, скажем y, мы получаем функцию регрессии или просто регрессию y на x. Аналогично можно получить регрессию x на y.

Регрессия (в теории вероятностей и математической статистики) – это зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин.

Функция регрессии изображается графически линией регрессии. Мера зависимости между величинами характеризуется коэффициентом корреляции или корреляционными отношениями.

Коэффициент Корреляции

2.1 Вычисление коэффициента корреляции

Коэффициентом корреляции r между случайными величинами x и y называется математическое ожидание произведения их нормированных отклонений:

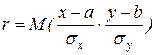, (1)

где 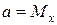, 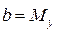– центры распределения величин x и y;

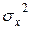и 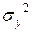– их дисперсии.

Коэффициент корреляции r может быть также записан в одной из следующих форм:

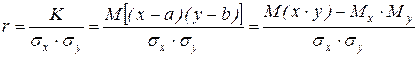. (2)

Величина 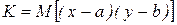называется корреляционным моментом или ковариацией.

Коэффициент корреляции представляет собой безразмерную величину, лежащую в пределах:

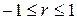. (3)

Для независимых x и y коэффициент корреляции 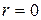. Равенство 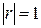говорит о наличии линейной функциональной зависимости между величинами x и y (т.е. означает, что каждому значению одной величины соответствует только одно значение другой величины): для возрастающей функции 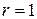, для убывающей функции .

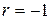Для экспериментального изучения зависимости между двумя величинами x и y производят некоторое количество n независимых испытаний (опытов, наблюдений). Результат i -го испытания дает пару значений 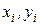(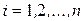). По этим значениям определяются точечные оценки как средних значений, так и коэффициента корреляции.

Несмещенными и состоятельными оценками средних значений a и b служат эмпирические средние значения:

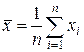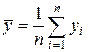, . (4)

Несмещенными и состоятельными оценками дисперси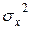й и 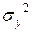служат эмпирические дисперсии:

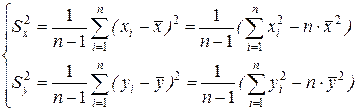(5)

Наконец, несмещенной и состоятельной оценкой корреляционного момента служит эмпирический корреляционный момент:

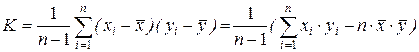. (6)

По этим оценкам рассчитывают эмпирический коэффициент корреляции:

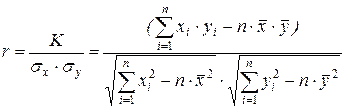. (7)

Эмпирический коэффициент корреляции не изменяется при изменении начала отсчета и масштаба измерения величин x и y. Это свойство позволяет существенно упростить вычисления с помощью выбора удобного начала отсчета 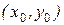и подходящих единиц масштаба: после замены

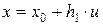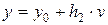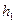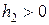, (, ), (8)

т.е. 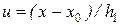, , 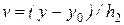эмпирический коэффициент корреляции вычисляется по формуле:

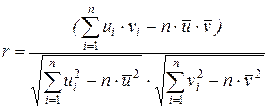, (9)

где , .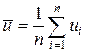

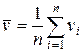Пример расчета коэффициента корреляции (пример 1).

Произведено n = 12 измерений значений x и y. В первых трех столбцах таблицы 1 даны различные пары измеренных значений (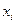, 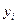) с указанием о количестве 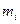измерений, в которых встретилась каждая точка (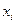, 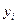). Для величины x выбрано начало отсчета 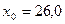, масштабный коэффициент 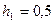. Для величины y соответственно 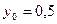, 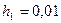. Таким образом, величины 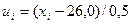, 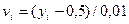принимают только целые значения. При подсчете сумм, входящих в формулу (9), каждое слагаемое учитывается столько раз, сколько раз оно встречается в таблице. Поэтому для расчета введены столбцы 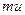, , 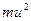, , 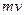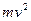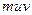. Во второй строке условно указан порядок действий, в последней строке подсчитаны суммы, необходимые для расчетов.

Таблица 1. – К расчету коэффициента корреляции.
x	y	m	u		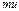	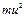v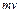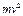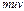
(1)	(2)	(3)	(4)	(5)=(3)(4)	(6)=(4)(5)	(7)	(8)=(3)(7)	(9)=(7)(8)
24,5 24,5 25,0 25,5 26,0 26,0 26,0	0,49 0,50 0,51 0,52 0,50 0,51 0,52		-3 -3 -2 -1	-9 -6 -2 -1		-1	-3		-2 -2
Суммы	n= 12	-			-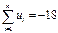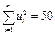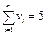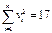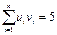

По полученным данным находим средние значения 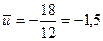, 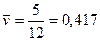и коэффициент корреляции:

.

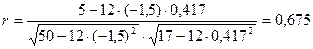Для контроля рекомендуется повторить расчет с другим началом отсчета.

2.2 Расчет коэффициента корреляции для корреляционной таблицы

Таблица 2 – Корреляционная решетка.
x y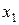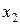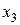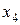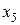
	–	–	–
	–	–
	–
	–				–
					–
				–	–

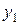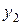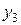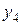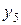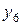Если весь диапазон изменения величины x разбит на интервалы равной длины, также как и весь диапазон изменения величины y, то результаты измерений удобно записывать в виде корреляционной таблицы (“корреляционной решетки”). В каждую клетку корреляционной таблицы проставляется только число измерений, результаты которых попали в данную клетку, а в заглавных строке и столбце указываются середины соответствующих интервалов.

Такова, например, таблица 2. При этом и весь расчет удобно проводить в той же корреляционной таблице. Поскольку здесь мы имеем дело с интервальными рядами, то в качестве масштабных коэффициентов 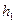и 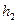следует выбирать длины соответствующих интервалов. При этом в новых переменных u и v середины интервалов оказываются просто номерами интервалов, отсчитываемыми от некоторого интервала.

Пример расчета коэффициента корреляции (пример 2).

Вычислить коэффициент корреляции по данным корреляционной таблицы 2.

Решение. Весь расчет проведен в таблице 3, причем этот расчет проведен уже в новых переменных u и v. В правом верхнем углу каждой клетки таблицы 3 выписано произведение 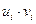, необходимое для подсчета суммы 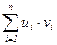. Все расчеты проведены в строках и столбцах, окаймляющих корреляционную таблицу.

Таблица 3 – К расчету коэффициента корреляции.
u v	-2	-1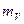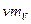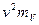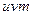
-2				-2	-4		-12		-20
-1				-1	-2		-13		-16
		-1
	-4	-2							-18
	-6	-3							-60
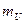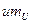	-22	-12
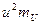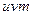	-60	-24			-28				-110

Во избежание ошибок в расчете, сумма 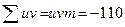подсчитана два раза – по столбцам и по строкам. С помощью подсчитанных сумм:

,

, ,

, ,

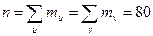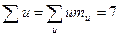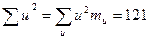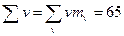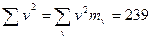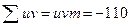
вычисляем средние арифметические значения:

, .

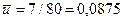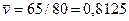По формуле (9) вычисляем коэффициент корреляции: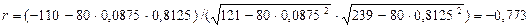

2.3 Доверительные оценки коэффициента корреляции

Даже для независимых величин эмпирический коэффициент корреляции может оказаться отличным от нуля вследствие случайного рассеивания результатов измерения. Поэтому следует проверить значимость коэффициента корреляции, т.е. проверить возможность отвергнуть гипотезу о некоррелированности рассматриваемых величин.

Значимость коэффициента корреляции проверяется путем сравнения абсолютной величины коэффициента корреляции, умноженной на 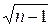, с его критическими значениями при заданной надежности вывода P. Критические значения произведения 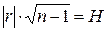для различных значений надежности вывода Р и различных чисел измерения n даны в таблице Приложения А. Если для коэффициента корреляции r произведение 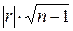окажется больше критического значения Н при некотором Р, то с надежностью вывода Р следует отвергнуть гипотезу о некоррелированности рассматриваемых величин.

В рассмотренных примерах расчета коэффициентов корреляции получим следующие доверительные оценки:

Пример 1. n =12, r = 0,675.

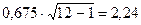. Это значение превосходит критическое H =1,91 при P =0,95. Следовательно, с надежностью вывода Р =0,95 можно утверждать о наличии корреляции между величинами x и y.

Пример 2. n =80, r = -0,773.

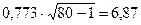, что значительно превосходит даже критическое значение Н =3,209 при надежности Р =0,999. В этом примере коэффициент корреляции является значимым, то есть с надежностью вывода, большей 0,999, можно утверждать о наличии сильной корреляции между величинами x и y.