Прямые регрессии

Эмпирическая прямая регрессия y на x имеет уравнение:

, (10)

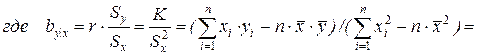
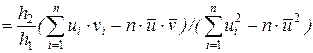(11)

есть эмпирический коэффициент регрессии y на x (обозначения см. в разделе 2).

Эмпирическая прямая регрессия x на y имеет уравнение:

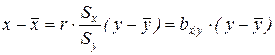, (12)

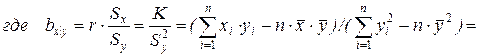
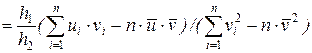(13)

есть эмпирический коэффициент регрессии x на y.

Обе прямые регрессии проходят через центр распределения – точку 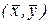. Коэффициенты регрессии имеют тот же знак, что и коэффициент корреляции и связаны соотношением 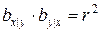. Прямые регрессии y на x и x на y совпадают только тогда, когда 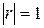, то есть в случае линейной функциональной зависимости между x и y.

Для ранее рассмотренного примера 1 получим:

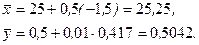
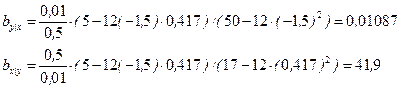
Уравнения эмпирических прямых регрессии:

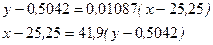
Графики прямых регрессии представлены на рисунке 1.

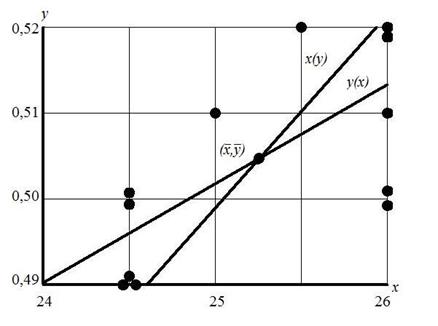
Рисунок 1 – Прямые регрессии