Имитация непрерывных случайных величин. Метод обратной функции

Метод обратной функции основывается на следующей теореме: если случайная величина 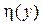имеет функцию плотности распределения 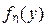, то

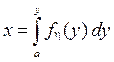
подчиняется равномерному закону распределения на отрезке [0, 1] (а – нижняя граница диапазона изменения случайной величины ).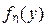

Таким образом, чтобы получить случайное число y_i с функцией плотности распределения 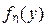необходимо решить интегральное уравнение

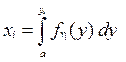
относительно верхнего предела интегрирования.

Пример. Для экспоненциального закона имеем

,

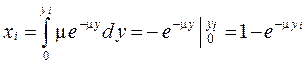или

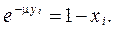
Откуда

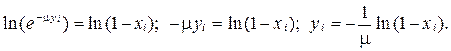
Достоинством метода обратной функции являются малые вычислительные затраты при реализации вычислений в аналитическом виде.

В качестве недостатков метода следует отметить следующие:

- использование численных методов решения интегрального уравнения приводит к ошибкам и большим затратам машинного времени;

- даже, когда интеграл берется в аналитическом виде, получаются формулы, содержащие функции вычисления логарифмов, возведения в степень, вычисления радикалов, что требует значительных затрат машинного времени.

Поэтому на практике пользуются другими, более универсальными, часто приближенными методами имитации непрерывных случайных величин.