Приближённый метод. Пусть закон распределения случайной величины 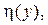 которую необходимо имитировать на ЭВМ, задан функцией плотности распределения
которую необходимо имитировать на ЭВМ, задан функцией плотности распределения 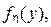 возможные значения которой лежат на отрезке [ a, b ]. Если этот отрезок с бесконечными границами, целесообразно перейти к усечённому распределению. Представим
возможные значения которой лежат на отрезке [ a, b ]. Если этот отрезок с бесконечными границами, целесообразно перейти к усечённому распределению. Представим 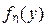 на участке [ a, b ] в виде кусочно-постоянной функции, т.е. отрезок [ a, b ] разобъем на n полуитервалов
на участке [ a, b ] в виде кусочно-постоянной функции, т.е. отрезок [ a, b ] разобъем на n полуитервалов 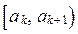 и будем считать
и будем считать 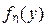 на каждом из них постоянной. Тогда случайную величину
на каждом из них постоянной. Тогда случайную величину 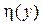 можно представить в виде
можно представить в виде
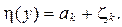
Величина 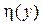 на
на 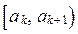 считается распределённой равномерно.
считается распределённой равномерно.
Для аппроксимации 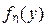 наиболее удобным способом, целесообразно разбить отрезок [ a, b ] на полуинтервалы
наиболее удобным способом, целесообразно разбить отрезок [ a, b ] на полуинтервалы 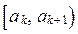 таким образом, чтобы вероятность попадания случайной величины
таким образом, чтобы вероятность попадания случайной величины 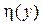 на любой из них была постоянной, т.е. не зависела от номера полуинтервала k. Для вычисления ak воспользуемся соотношением
на любой из них была постоянной, т.е. не зависела от номера полуинтервала k. Для вычисления ak воспользуемся соотношением
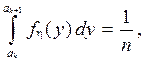
где n – количество полуинтервалов.
Процедура имитации предполагает следующее:
- генерируется значение xi случайной равномерно распределённой на отрезке [0, 1] величины ξ(x);
- с помощью xi выбирается полуинтервал 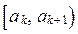 (путём моделирования дискретной случайной величины, принимающей n равновероятных значений);
(путём моделирования дискретной случайной величины, принимающей n равновероятных значений);
- генерируется следующее значение xi +1 случайной равномерно распределённой на отрезке [0, 1] величины ξ (x), которое масштабируется с целью приведения его к полуинтервалу 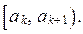
Таким образом, значение xi +1 становится значением случайной величины 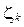 , равномерно распределённой на полуинтервале
, равномерно распределённой на полуинтервале 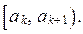
Затем случайные числа с требуемым законом распределения вычисляются по формуле
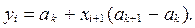
 2015-05-20
2015-05-20 593
593








