Получение случайных чисел с заданным законом распределения. Квазиравномерные псевдослучайные числа используются в качестве исходного материала для формирования любых вероятностных объектов. Такими объектами, в первую очередь, являются случайные события, наступающие с заданной вероятностью и случайные величины с заданными законами распределения.
Моделирование случайного события (реализация жребия). Пусть требуется моделировать событие A, наступающее с заданной вероятностью 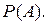
Рассмотрим случайную величину ξ (x), распределённую равномерно на отрезке [0, 1]. Считается, что событие A произошло, если 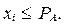 Легко видеть, что вероятность события A равна
Легко видеть, что вероятность события A равна 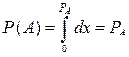 .
.
Таким образом, моделирование события A, вероятность наступления которого 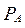 сводится к следующей процедуре:
сводится к следующей процедуре:
1. Выбирается очередное значение xi случайной величины ξ (x).
2. Проверяется неравенство 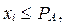 устанавливающее принадлежность xi отрезку [0, PA ].
устанавливающее принадлежность xi отрезку [0, PA ].
Если xi удовлетворяет неравенству 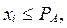 то событие A наступило, в противном случае – не наступило (наступило противоположное событие A).
то событие A наступило, в противном случае – не наступило (наступило противоположное событие A).
Имитация дискретной случайной величины с заданным законом распределения. Пусть величина 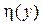 принимает возможные значения
принимает возможные значения 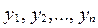 с вероятностями
с вероятностями 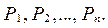
В качестве значения случайной величины 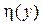 будет принято: y 1, если
будет принято: y 1, если 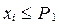 ; y 2, если
; y 2, если 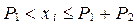 ; y 3, если
; y 3, если 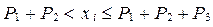 и т.д.
и т.д.
Другими словами, если 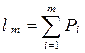 , то при
, то при 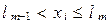 случайная величина
случайная величина 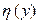 принимает значение
принимает значение 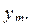
 2015-05-20
2015-05-20 575
575








