Краткие теоретические сведения. При изменении технического состояния автомобиля различные неисправности могут частично сопровождаться одинаковыми диагностическими параметрами

При изменении технического состояния автомобиля различные неисправности могут частично сопровождаться одинаковыми диагностическими параметрами. Описание диагнозов удобно свести в матрицу, обозначая наличие признака «1», а отсутствие – «0» (Таблица 6)

Таблица 6 – Диагностическая матрица

Диагнозы	Диагностические параметры
S1	S2	S3	S4	S5

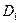
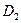
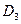
На основании подобных матриц делались попытки создавать электрические приборы для автоматической постановки диагнозов, содержащие набор тумблеров (включателей) и сигнальных лампочек (по числу диагнозов). При соответствующем строке диагноза сочетании включенных и выключенных тумблеров в приборе зажигается лампочка данного диагноза. Однако, на практике такие приборы оказались неработоспособные.

Говоря об отсутствии или наличии некоторого диагностического признака, имеется в виду, что диагностический параметр меньше или больше допустимого значения диагностического параметра S_пд. Контролируемые диагностические параметры имеют случайный разброс из-за ошибок измерения, случайного сочетания режимов работы разных элементов автомобиля и т. п. Поэтому наличие или отсутствие диагностического признака при определенном диагнозе 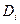не является достоверным событием («1» или «0»), а наблюдается с некоторой условной вероятностью .

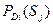Наблюдая за большой группой автомобилей можно установить, как часто встречаются интересующие нас диагнозы - 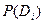, и с какой вероятностью при этих диагнозах встречаются принятые для разрабатываемой системы диагностические параметры - 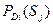. Для определения вероятностей наблюдения различных признаков, можно искусственно вносить в автомобиль интересующие неисправности (нарушать регулировки и т. п.).

Пусть результаты статистических исследований будут представлены таблицей 7.

Таблица 7 – Диагностическая матрица

Диагноз	Вероятности диагностических параметров	Вер. диагноза
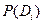
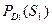
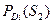
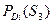
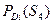
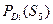
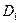
	PD 1 (S 1 )	PD 1 (S 2 )	PD 1 (S 3 )	PD 1 (S 4 )	PD 1 (S 5 )	0,05
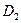
	PD 2 (S 1 )	PD 2 (S 2 )	PD 2 (S 3 )	PD 2 (S 4 )	PD 2 (S 5 )	0,10
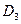
	PD 3 (S 1 )	PD 3 (S 2 )	PD 3 (S 3 )	PD 3 (S 4 )	PD 3 (S 5 )	0,30
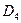
	PD 4 (S 1 )	PD 4 (S 2 )	PD 4 (S 3 )	PD 4 (S 4 )	PD 4 (S 5 )	0,55

Поставим диагноз для автомобиля с комплексом признаков: 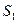, 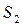и 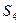, остальные диагностические параметры не наблюдаются, т. е.

,

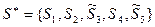где 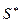- обозначение обобщенного диагностического параметра;

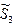и 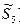- обозначение диагностических параметров, значения которых не выходят за предельно допустимые.

Расчет наиболее вероятного диагноза можно произвести по известной в теории вероятностей формуле Бейеса, рассмотрим ее типичный вывод.

Пусть в урне находится 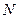шаров, среди которых 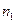- пустотелые, из них 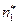- белые, и 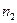- сплошные, из них 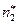- белые (остальные пустотелые и сплошные шары черные).

Вероятность вынуть пустотелый шар (события )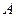

.

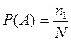Вероятность вынуть белый шар (события )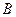

.

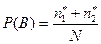Вероятность, что вынутый пустотелый шар окажется белым,

.

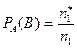Вероятность, что вынутый белый шар окажется пустотелым,

.

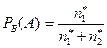Вероятность, что шар будет белым и пустотелым (совместное наблюдение двух событий определяется произведением вероятностей)

.

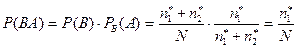Вероятность, что шар будет пустотелым и белым

.

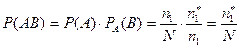Поскольку 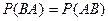, можно записать

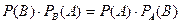, отсюда формула Бейеса

.

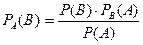Применительно к диагностике формулу Бейеса можно записать

,

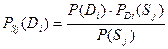где 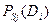- вероятность 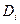- го диагноза при наблюдении 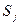-го параметра;

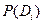- вероятность 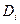- го диагноза;

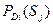- вероятность наблюдения 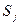- го параметра при диагнозе ;

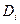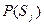- вероятность наблюдения 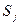- го параметра по всем диагнозам.

При постановке диагноза по комплексу признаков, формула будет записываться аналогично, но вместо единичного параметра 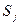будет рассматриваться комплекс параметров .

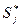Вероятность совместного наблюдения независимых признаков, составляющих анализируемый комплекс диагностических параметров, можно выразить произведением вероятностей наблюдения каждого параметра при рассматриваемом диагнозе 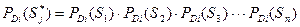. Если в комплексе некоторые признаки отсутствуют, то в произведение ставят вероятность отсутствия диагностического параметра .

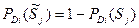Вероятность наблюдения комплекса признаков по всем диагнозам определяют по формуле полной вероятности (как математическое ожидание)

.

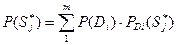Условия задания 3. Рассчитать вероятности диагнозов для заданного комплекса диагностических параметров 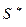, принятого по таблице 8 используя диагностическую матрицу (таблица 9).

Таблица 8 – Комплексные диагностические параметры

Последняя цифра зачетной книжки
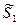
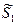
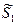
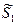
S*					S1	S1	S1	S1	S1	S1
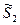
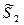
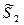
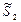
	S2	S2	S2				S2	S2	S2
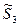
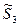
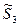
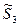
S3		S3	S3		S 3	S3			S3
S4	S4		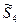S4	S4		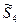S4		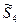S4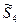
S5	S5	S5		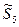S5	S5		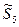S5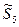

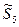
Таблица 9 – Диагностическая матрица

Диагноз	Вероятности диагностических параметров	Вер. диагноза
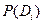
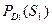
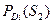
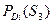
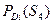
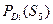
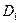
	1,0	0,8	0,9	1,0	0,1	0,05
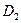
	0,9	0,7	0,8	0,0	0,2	0,10
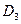
	0,6	0,1	0,9	0,1	0,8	0,30
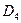
	0,1	0,1	0,0	0,1	0,0	0,55