Каковы особенности определения постоянных интегрирования в цепях второго порядка? Показать на конкретном примере

Ответ: Цепи второго порядка содержат два реактивных элемента; это могут быть две индуктивности, две емкости или емкость с индуктивностью. Кроме того, цепь включает некоторое количество резистивных элементов и независимых источников энергии, которые для простоты анализа будем считать стационарными. В зависимости от наличия тех или иных реактивных элементов, решение задачи следует искать или для переменной состояния i_L (t), или для u_C (t). Форма записи решения определена общей теорией:

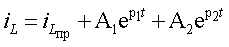(3.17)

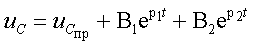(3.18)

где p₁ и p₂ - корни характеристического уравнения. Поиск решения выполняется в той же последовательности, что и для цепей первого порядка: 1. Находят корни характеристического уравнения. Они могут быть вещественными разными и отрицательными или вещественными кратными и отрицательными или комплексно-сопряженными с отрицательной вещественной частью; 2. Из анализа цепи после коммутации определяют принужденную составляющую режима 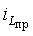или 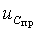, что можно сделать, если в цепи продолжают действовать стационарные источники питания; 3. Исследуя основные и неосновные начальные условия, находят постоянные интегрирования 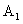, 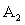или 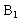, 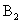. Рассмотрим подробнее каждый шаг решения. 1. Определение корней характеристического уравнения. Характеристическое уравнение может быть получено классическим методом путем составления системы уравнений по законам Кирхгофа с последующим сведением этой системы к одному дифференциальному уравнению второго порядка. Этот способ подробно описан в учебной литературе и здесь не рассматривается. Как показывают примеры, рассмотренные ранее, этот путь сопровождается достаточно громоздкими преобразованиями. Было замечено, что характеристическое уравнение содержится внутри

функции входного сопротивления как некоторый инвариант, присущий данной цепи. Рассмотрим этот способ получения характеристического уравнения путем исследования входного сопротивления на примере цепи, представленной на рис.3.13а. Будем считать, что цепь питается от источника постоянного тока и содержит два резистивных сопротивления, индуктивность и емкость. После коммутации (t >0) (ключ S замыкается) переходный процесс в цепи, изображенной на рис.3.13б, развивается за счет независимого источника тока, а также за счет энергии, запасенной в реактивных элементах цепи. Свободная составляющая режима, определяемая корнями характеристического уравнения, не зависит от внешнего источника питания, а определяется только параметрами элементов ветвей и способом их соединения. Точно так же не зависит от внешних источников питания и функция входного сопротивления [1]. Поэтому возникает идея поискать корни характеристического уравнения внутри функции входного сопротивления. На рис.3.13в и рис.3.13г представлены комплексные схемы замещения цепи, которые следует составить для определения входного сопротивления со стороны

первой и третьей ветви, где .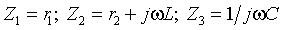

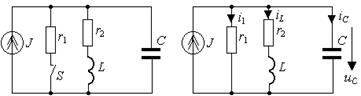
а) б)

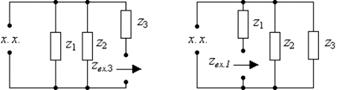
в) г)

Рис. 3.13. Схема RLC -цепи второго порядка:

а)исходная цепь; б)схема после коммутации; в)входное сопротивление со стороны третьей ветви; г)входное сопротивление со стороны первой ветви. Объединяя параллельно и последовательно соединенные ветви, найдем входные сопротивления со стороны обозначенных зажимов

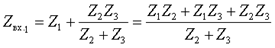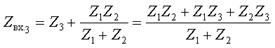Числители полученных выражений совпадают, а знаменатели различны. Аналогичный результат получим, если найдем входное сопротивление со стороны второй ветви. Следовательно, числитель входного сопротивления со стороны любой ветви является некоторым расчетным инвариантом, определяемым топологией цепи. Числитель этого инварианта при замене комплексной переменной j ω на p совпадает с характеристическим полиномом. Используя эту замену и, приравнивая числитель к нулю, получим характеристическое уравнение:

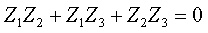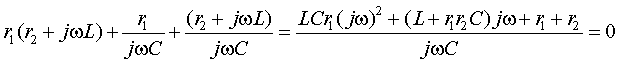или

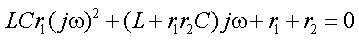После замены в числителе переменной j ω на p и деления на коэффициент при старшем члене получим уравнение второй степенин.Найдем корни этого уравнения:

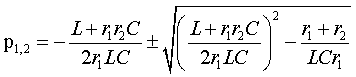18)Что представляет собой постоянная времени цепи 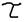? Как её определяют расчётным путём?

Ответ: Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U, в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения U_C и определится выражением:

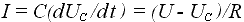. Тогда напряжение U_C на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте: U_C = U( 1 - e ^-t/RC )

При t = RC, напряжение на конденсаторе составит U_C = U( 1 - e ^-1 ) = U( 1 - 1 /e).
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.

Постоянная времени τ = RC

За время τ конденсатор зарядится до (1 - 1 /e)*100% ≈ 63,2% значения U.
За время 3 τ напряжение составит (1 - 1 /e ³)*100% ≈ 95% значения U.
За время 5 τ напряжение возрастёт до (1 - 1 /e ⁵)*100% ≈ 99% значения U.

Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R, тогда в цепи пойдёт ток разряда конденсатора.

Напряжение на конденсаторе при разряде будет составлять U_C = Ue ^-t/τ = U/e ^t/τ.

За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1 /e *100% ≈ 36.8% значения U.
За время 3 τ конденсатор разрядится до (1 /e ³)*100% ≈ 5% от значения U.
За время 5 τ до (1 /e ⁵)*100% ≈ 1% значения U.

Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.

19)Привести известные способы определения постоянной времени 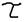по осциллограме переходного процесса.

Ответ: Общий подход к расчету переходных процессов в таких цепях основан на применении теоремы об активном двухполюснике: ветвь, содержащую накопитель, выделяют из цепи, а оставшуюся часть схемы рассматривают как активный двухполюсник А (эквивалентный генератор) (см. рис.1, а) со схемой замещения на рис. 1,б.

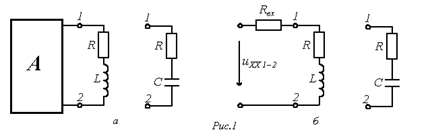
Совершенно очевидно, что постоянная времени здесь для цепей с индуктивным элементом определяется, как: 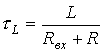, и с емкостным, как: 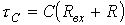, где 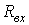- входное 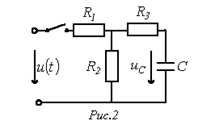сопротивление цепи по отношению к зажимам 1-2 подключения ветви, содержащей накопитель энергии. Например, для напряжения на конденсаторе в цепи на рис. 2 можно записать:

,

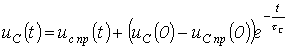где в соответствии с вышесказанным:

.

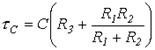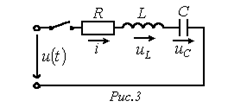Переходные процессы при подключении последовательной R-L-C-цепи к источнику напряжения: Рассмотрим два случая: а) ;

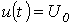б) .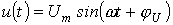

Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать:

.

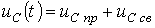(1)

Тогда для первого случая принужденная составляющая этого напряжения:

.

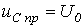(2)

Характеристическое уравнение цепи: 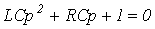, решая которое, получаем:

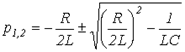. В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:

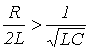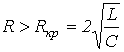1. или , где 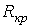- критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер. В этом случае:

.

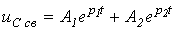(3)

2. 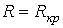- предельный случай апериодического режима. В этом случае 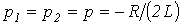и

.

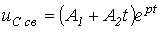(4)

3. 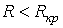- периодический (колебательный) характер переходного процесса.

В этом случае 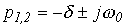и

,

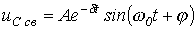(5)

где 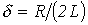- коэффициент затухания; 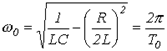- угловая частота собственных колебаний; 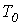- период собственных колебаний. Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать: 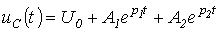. Для нахождения постоянных интегрирования, учитывая, что в общем случае 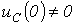и в соответствии с первым законом коммутации: 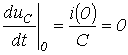, запишем для t=0 два уравнения:

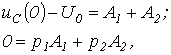решая которые, получим: 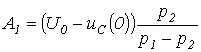; 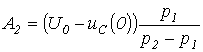. Таким образом, .

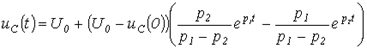Тогда ток в цепи: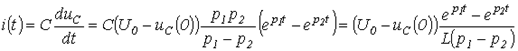

и напряжение на катушке индуктивности: .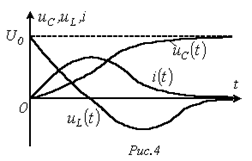

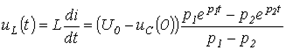На рис. 4 представлены качественные кривые 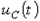, 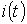и 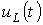, соответствующие апериодическому переходному процессу при 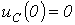. Для критического режима на основании (2) и (4) можно записать

.

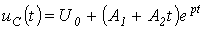При 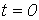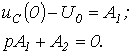Таким образом: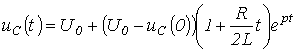

и .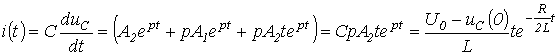

Для колебательного переходного процесса в соответствии с (2) и (5) имеем: 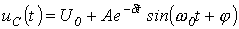. Для нахождения постоянных интегрирования запишем 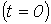: 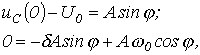откуда 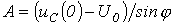и 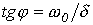. Тогда:

.

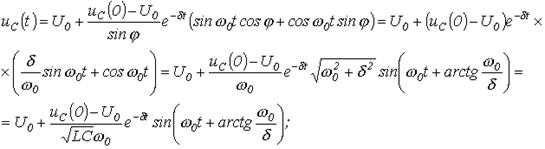
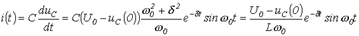
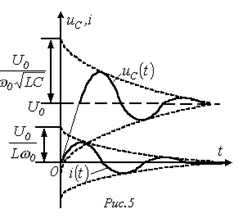
На рис. 5представлены качественные кривые 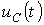и 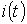, соответствующие колебательному переходному процессу при 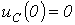. При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым:

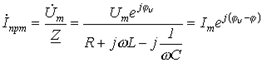
И 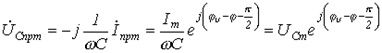, где ; ; .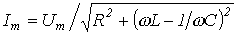

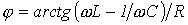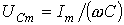Таким образом, 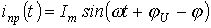и 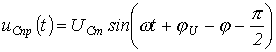. Здесь также возможны три режима:

1. 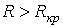;	2.	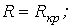3.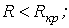

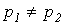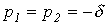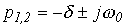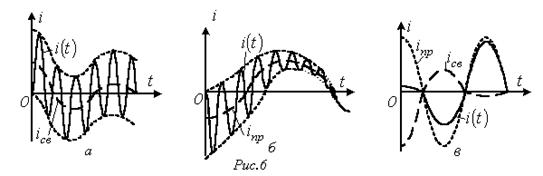
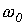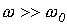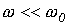Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой . При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: 1 - ; 2 - ; 3 - 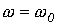, - которые представлены на рис. 6,а…6,в соответственно.