Ответ: Рассчитать напряжение на конденсаторе и ток в катушке в схеме, приведенной на рис. 21, при закорачивании сопротивления 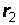 , если
, если 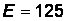 В,
В, 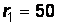 Ом,
Ом, 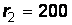 Ом,
Ом, 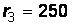 Ом,
Ом, 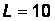 мГн,
мГн, 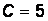 мкФ.
мкФ.
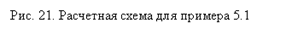
|

Решение: 1. 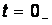 . Анализ цепи до коммутации:
. Анализ цепи до коммутации: 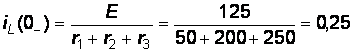 А,
А, 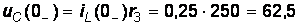 В. 2.
В. 2. 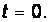 Определение начальных условий.
Определение начальных условий.
По законам коммутации: 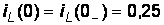 А,
А, 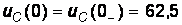 В.
В.
Для послекоммутационной цепи составим уравнения по законам Кирхгофа:

Из уравнения (6), записанного для момента 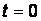 , определим напряжение на катушке, а, решая совместно уравнения (5) и (7) для момента коммутации, найдем ток через конденсатор:
, определим напряжение на катушке, а, решая совместно уравнения (5) и (7) для момента коммутации, найдем ток через конденсатор:
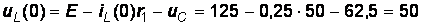 В,
В,
 А. Используя уравнения связи
А. Используя уравнения связи 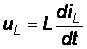 и
и 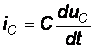 , найдем скорости изменения тока на катушке индуктивности и напряжения на конденсаторе для момента времени
, найдем скорости изменения тока на катушке индуктивности и напряжения на конденсаторе для момента времени 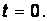 Это будет являться необходимым условием для нахождения постоянных интегрирования:
Это будет являться необходимым условием для нахождения постоянных интегрирования:
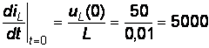 А/с, (8)
А/с, (8) 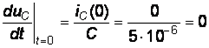 В/с. (9) 3. Общее решение неоднородного линейного дифференциального уравнения, составленного для цепи после замыкания ключа, может быть представлено в виде:
В/с. (9) 3. Общее решение неоднородного линейного дифференциального уравнения, составленного для цепи после замыкания ключа, может быть представлено в виде: 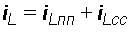 или
или 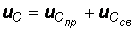 .
.
4. 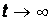 .Определение принужденной составляющей:
.Определение принужденной составляющей: 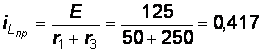 А,
А,
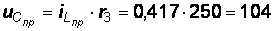 В. 5.
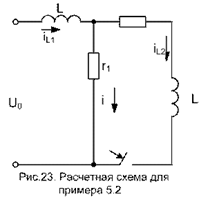
В. 5. 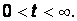 Определение свободной составляющей. Составим характеристическое уравнение по методу входного сопротивления. Для этого замыкаем накоротко источник эдс и размыкаем ветвь, содержащую конденсатор.
Определение свободной составляющей. Составим характеристическое уравнение по методу входного сопротивления. Для этого замыкаем накоротко источник эдс и размыкаем ветвь, содержащую конденсатор.

|
Схема для написания характеристического уравнения приведена на рис. 22. Рис. 22. Схема для написания характеристического уравнения в примере 5.1
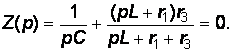
|
Относительно разомкнутых зажимов определим сопротивление, заменяя элементы L на pL, С на 1/рС. После того как полученное уравнение приведем к общему знаменателю и числитель приравняем к нулю, уравнение примет вид: 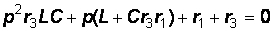
или в приведенном виде: 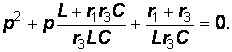 (10) Подставим в уравнение (10) численные значения:
(10) Подставим в уравнение (10) численные значения:
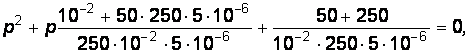
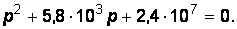 Решая квадратное уравнение, найдем его корни:
Решая квадратное уравнение, найдем его корни:
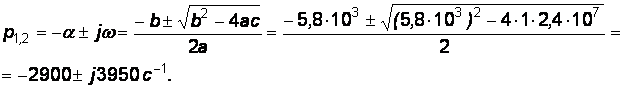 Процесс носит колебательной характер, затухающий по экспоненциальному закону, а свободные составляющие примут вид:
Процесс носит колебательной характер, затухающий по экспоненциальному закону, а свободные составляющие примут вид:
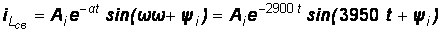 ,
,
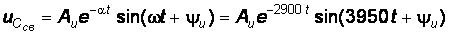 , где
, где 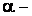 коэффициент затухания;
коэффициент затухания; 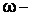 угловая частота собственных колебаний в контуре. 6. Определение постоянных интегрирования. Уравнения для определения свободных составляющих содержат по две постоянных интегрирования:
угловая частота собственных колебаний в контуре. 6. Определение постоянных интегрирования. Уравнения для определения свободных составляющих содержат по две постоянных интегрирования: 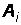 – характеризует амплитуду искомой величины,
– характеризует амплитуду искомой величины, 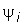 – ее начальную фазу. Для нахождения
– ее начальную фазу. Для нахождения 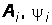 необходимо решить систему уравнений:
необходимо решить систему уравнений:


Запишем эти уравнения для момента времени 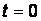 , учитывая (8), получим:
, учитывая (8), получим:
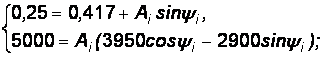
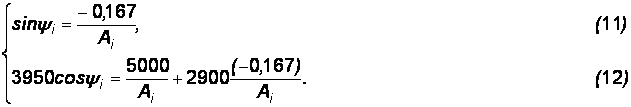
Из уравнения (12) выразим 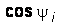 , а затем (11) разделим на (12), получим
, а затем (11) разделим на (12), получим 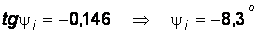 . Подставляя в (11) значение
. Подставляя в (11) значение 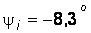 , определим
, определим
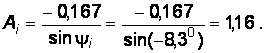 Уравнение для
Уравнение для 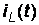 , А, имеет вид:
, А, имеет вид:
 . Аналогично находятся
. Аналогично находятся 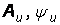 – необходимо решить систему уравнений:
– необходимо решить систему уравнений:
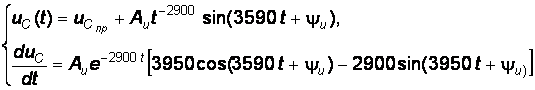
Для момента времени 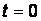 , учитывая, что
, учитывая, что 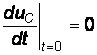 В/с, получим:
В/с, получим: 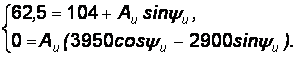
Решая последнюю систему уравнений, найдем 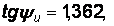
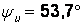 , Аu = –51,49 В.
, Аu = –51,49 В.
 Уравнение для
Уравнение для 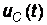 , В, имеет вид:
, В, имеет вид: 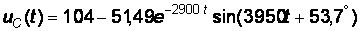 .
.
 2015-05-20
2015-05-20 790
790








