В чём особенность составления уравнений для определения постоянных интегрирования в цепях второго порядка? Показать на конкретном примере

Ответ: Цепи второго порядка содержат два реактивных элемента; это могут быть две индуктивности, две емкости или емкость с индуктивностью. Кроме того, цепь включает некоторое количество резистивных элементов и независимых источников энергии, которые для простоты анализа будем считать стационарными. В зависимости от наличия тех или иных реактивных элементов, решение задачи следует искать или для переменной состояния i_L (t), или для u_C (t). Форма записи решения определена общей теорией:

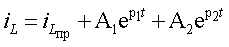
(3.17)

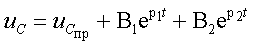
(3.18)

где p₁ и p₂ - корни характеристического уравнения. Поиск решения выполняется в той же последовательности, что и для цепей первого порядка: 1. Находят корни характеристического уравнения. Они могут быть вещественными разными и отрицательными или вещественными кратными и отрицательными или комплексно-сопряженными с отрицательной вещественной частью; 2. Из анализа цепи после коммутации определяют принужденную составляющую режима 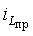или 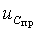, что можно сделать, если в цепи продолжают действовать стационарные источники питания; 3. Исследуя основные и неосновные начальные условия, находят постоянные интегрирования 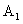, 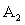или 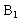, 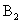. Рассмотрим подробнее каждый шаг решения. 1. Определение корней характеристического уравнения. Характеристическое уравнение может быть получено классическим методом путем составления системы уравнений по законам Кирхгофа с последующим сведением этой системы к одному дифференциальному уравнению второго порядка. Этот способ подробно описан в учебной литературе и здесь не рассматривается. Как показывают примеры, рассмотренные ранее, этот путь сопровождается достаточно громоздкими преобразованиями. Было замечено, что характеристическое уравнение содержится внутри

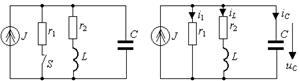
функции входного сопротивления как некоторый инвариант, присущий данной цепи. Рассмотрим этот способ получения характеристического уравнения путем исследования входного сопротивления на примере цепи, представленной на рис.3.13а. Будем считать, что цепь питается от источника постоянного тока и содержит два резистивных сопротивления, индуктивность и емкость. После коммутации (t >0) (ключ S замыкается) переходный процесс в цепи, изображенной на рис.3.13б, развивается за счет независимого источника тока, а также за счет энергии, запасенной в реактивных элементах цепи. Свободная составляющая режима, определяемая корнями характеристического уравнения, не зависит от внешнего источника питания, а определяется только параметрами элементов ветвей и способом их соединения. Точно так же не зависит от внешних источников питания и функция входного сопротивления [1]. Поэтому возникает идея поискать корни характеристического уравнения внутри функции входного сопротивления. На рис.3.13в и рис.3.13г представлены комплексные схемы замещения цепи, которые следует составить для определения входного сопротивления со стороны

первой и третьей ветви, где .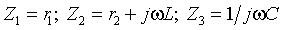

а) б)

в) г)

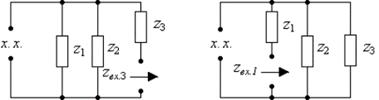
Рис. 3.13. Схема RLC -цепи второго порядка:

а)исходная цепь; б)схема после коммутации; в)входное сопротивление со стороны третьей ветви; г)входное сопротивление со стороны первой ветви. Объединяя параллельно и последовательно соединенные ветви, найдем входные сопротивления со стороны обозначенных зажимов

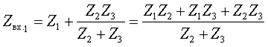
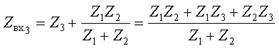
Числители полученных выражений совпадают, а знаменатели различны. Аналогичный результат получим, если найдем входное сопротивление со стороны второй ветви. Следовательно, числитель входного сопротивления со стороны любой ветви является некоторым расчетным инвариантом, определяемым топологией цепи. Числитель этого инварианта при замене комплексной переменной j ω на p совпадает с характеристическим полиномом. Используя эту замену и, приравнивая числитель к нулю, получим характеристическое уравнение:

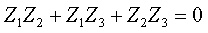
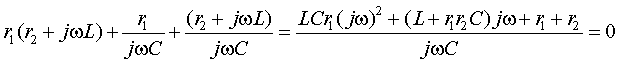
или

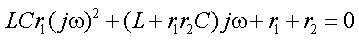
После замены в числителе переменной j ω на p и деления на коэффициент при старшем члене получим уравнение второй степенин.Найдем корни этого уравнения

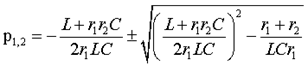
На основании этого анализа сформулируем порядок получения характеристического уравнения цепи: а. Для времени t >0 следует изобразить комплексную расчетную цепь; б. Исключить из схемы все независимые источники энергии: источники тока разомкнуть, источники напряжения замкнуть накоротко. Найти входное сопротивление со стороны любой ветви и записать это выражение в виде дробно-рациональной функции, где в числителе и в знаменателе образуются полиномы по степеням j ω

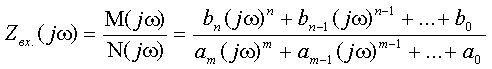
в. Числитель полученного выражения, совпадающий с характеристи-ческим полиномом, приравнять к нулю, предварительно заменив переменную j ω на p. Найти корни характеристического уравнения и записать решение для искомой переменной состояния в виде (3.17) или (3.18).

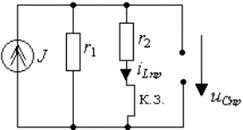
Рис. 3.14. Схема для определения принужденных составляющих режима

2. Определение принужденной составляющей режима при стационарном воздействии находят для момента времени t = ∞, когда переходный процесс в цепи уже закончен. Для рассматриваемого в примере режима постоянного тока исследуемая схема приведена на рис.3.14, где индуктивность заменена короткозамкнутой перемычкой, а емкость разрывом. Используя правило деления тока на части, найдем:

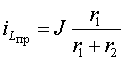
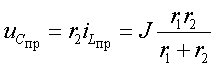
3. Постоянные интегрирования A₁ и A₂ (или B₁ и B₂) можно найти на основании основных и неосновных начальных условий. Основные начальные условия определяются законами коммутации по схеме докоммутационного состояния цепи. Для рассматриваемого примера такая схема приведена на рис.3.15а, из анализа которой следует:

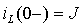
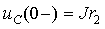
что дает одно уравнение для определения постоянных интегрирования:

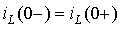
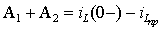
(3.19)

или

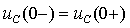
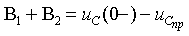
(3.20)

Второе уравнение получим из анализа неосновных начальных условий, которые определяются исследованием энергетического состояния цепи для момента времени t = 0+. К этим условиям относят численные значения напряжений на индуктивностях и токов в емкостях в первый момент после коммутации, которые претерпевают скачок в момент коммутации и связаны с переменными состояния известными дифференциальными соотношениями:

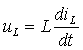
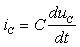
(3.21)

Для рассматриваемого примера анализируемая схема цепи представлена на рис.3.15б. Особенностью этой цепи по сравнению с исходной является появление двух новых внутренних источников энергии, которые обусловлены законами коммутации и перешли в анализируемую схему из предыдущей схемы рис.3.15а. Фактически исследуется цепь постоянного тока, содержащая резистивные элементы, а также внешние и внутренние источники энергии. Расчет цепи может выполняться любым методом. Целесообразно, например, использовать законы Кирхгофа или метод наложения.

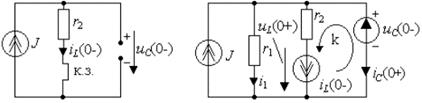
а) б)

Рис. 3.15. Схема для анализа состояния цепи:

а)до коммутации; б)в первый момент после коммутации. Составим уравнение равновесия напряжений для контура k, который включает искомое напряжение 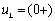на источнике тока 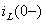. Ток в сопротивлении 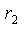определен этим источником, поэтому напряжение u _L (0+) находится сразу

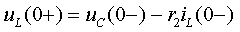
После подстановки найденных ранее значений получим .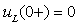

На основании первого закона Кирхгофа, найдем ток в емкости :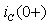

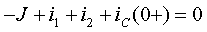
где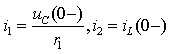

После подстановки в уравнение равновесия получим:

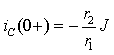
Используя общий вид решения (3.17) и (3.18), найдем:

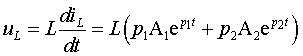
(3.22)

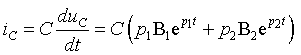
(3.23)

Для исследуемого момента времени t = 0+ имеем равенства:

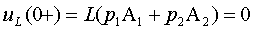
(3.24)

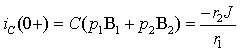
(3.25)

Объединяя уравнения (3.19) и (3.24) в систему, найдем постоянные интегрирования A₁ и A₂:

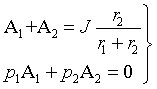
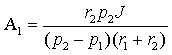
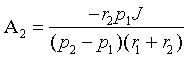
Подстановка значений A₁ и A₂ в выражения (3.17) и (3.22) позволяет окончательно записать ток 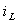и напряжение 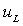в индуктивности. Другие токи и напряжения могут быть найдены путем решения обратной задачи:

1.Напряжение на втором резистивном элементе:

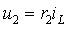
2.Напряжение на емкости:

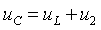
3.Ток в емкости:

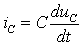
4.Ток в первом резистивном элементе:

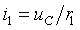
Решение задачи через определение переменной состояния 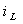на этом можно считать законченным. Второй путь решения заключается в первоначальном определении напряжения на емкости, что предполагает нахождение постоянных интегрирования B₁ и B₂. Это можно осуществить, объединив в систему уравнения (3.20) и (3.25):

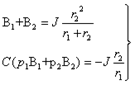
Решение системы:

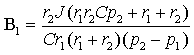
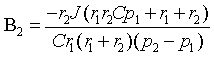
Подставив постоянные интегрирования B₁ и B₂ в выражения (3.18) и (3.23), окончательно найдем напряжение 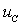и ток 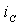в емкости. Решением обратной задачи определим: 1.Ток в первом резистивном элементе:

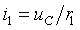
2. Ток в индуктивности:

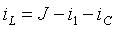
3.Напряжение на индуктивности:

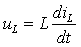
4.Напряжение на втором резистивном элементе:

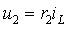
Задача решена.

26)Что представляет коэффициент затухания 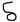в случае колебательного характера переходной величины? Как он определяется расчётным путём и по осциллограмме?

Ответ: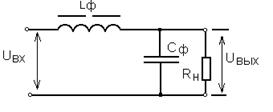

При соблюдении условия Х_др > Х_с реакция фильтра будет индуктивного характера. Дроссель и конденсатор, используемые совместно, более эффективно выполняют функции сглаживания, чем при их раздельном включении, если выполняются неравенства: Х_др >> R_н и Х_с << R_н. Получим выражение для коэффициента сглаживания фильтра через параметры схемы замещения:

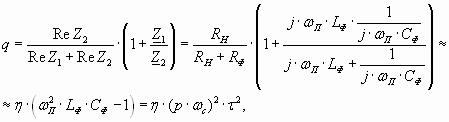Фильтр используется при большой мощности нагрузки. К достоинствам фильтра относится: малые габаритные размеры, малая зависимость коэффициента сглаживания от изменений тока нагрузки (различный характер зависимости q от Iн для реактивных элементов взаимно компенсирует влияние). Недостатки: в таких фильтрах возникают переходные процессы, усложняющие работу, как потребителя, так и источника питания, дроссели фильтров имеют большие габаритные размеры и массу, а их индуктивность, следовательно, коэффициенты сглаживания зависят от тока нагрузки. При включении и отключении сети, а также при резких изменениях нагрузки в фильтре возникают переходные процессы, которые могут привести к перенапряжениям и броскам тока в элементах фильтра и выпрямителя. Возникновение переходных процессов связано с изменением во времени запасов электромагнитной энергии, накапливаемой в таких энергоемких элементах, как катушки индуктивности (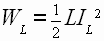) и конденсаторы фильтра (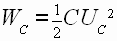). Пр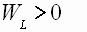и или 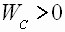разряд индуктивности или конденсатора фильтра происходит за некоторый интервал времени (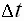), который определяет время переходного процесса. Несмотря на малую продолжительность этих процессов, они могут быть причиной выхода из строя вентилей из-за резкого возрастания обратного напряжения и прямого тока, а также пробоя конденсаторов или изоляции дросселей и силового трансформатора. Переходные процессы могут носить колебательный характер. В этом случае их можно рассматривать как свободные, затухающие при подключении фильтра к источнику постоянного тока. Собственная частота этих колебаний определяется выражением: 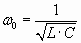На рисунке представлена графическая зависимость переходного процесса при включении источника питания:

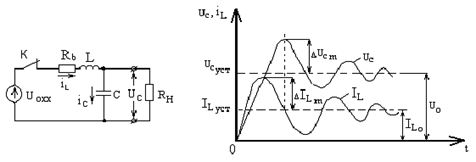
Переходные процессы в контуре описываются уравнением: 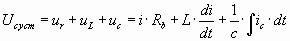, где U_{с уст} – напряжение выпрямителя на холостом ходу (при отключенной нагрузке), i = i_н + i_с – ток выпрямителя во время переходного процесса, i_н и i_с – соответственно токи нагрузки и конденсатора, R_b = r_тр + R_i + R_др – внутреннее сопротивление выпрямителя: трансформатора, диодов и дросселя фильтра. Математический анализ выше приведенного уравнения позволяет определить сдвиг по фазе между максимумами тока i_L и напряжения U_c, который составляет 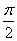. Максимальное отклонение напряжения на конденсаторе 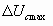зависит от коэффициента затухания колебательного процесса: 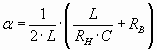. Относительная величина перенапряжения на конденсаторе 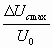определяется из графика в зависимости от отношения .

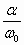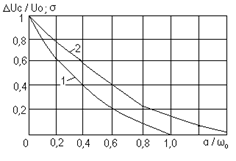Перенапряжения, возникающие в фильтре, тем больше, чем больше индуктивность дросселя L и чем меньше емкость С. Для идеального выпрямителя при R_b = 0 и отключенной нагрузке (R_н = 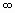) отношения 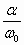= 0, 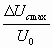= 1, т.е. предельное значение напряжения на конденсаторе равно:

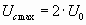. Если максимальное напряжение на конденсаторе 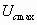превышает допустимое значение, а уменьшить индуктивность дросселя нельзя из-за необходимости обеспечения требуемого коэффициента сглаживания, то для уменьшения перенапряжения последовательно с дросселем нужно включить добавочный, так называемый пусковой резистор с сопротивлением R_пуск. При этом активное сопротивление выпрямителя возрастет на его величину и коэффициент затухания α увеличится, что приводит к уменьшению 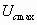. Для мощных выпрямителей допустимой считается величина перенапряжений на конденсаторе до 20%. При резких изменениях сопротивления нагрузки от R_н до R^/_н в фильтре также создаются перенапряжения и броски тока. Максимальное значение перенапряжения на конденсаторе определяется выражением:

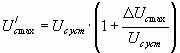где отношение 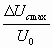определяется из приведенного выше графика в зависимости от произведения:

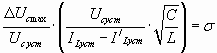При нахождении величины α вместо сопротивления нагрузки R_н в формулу надо подставить значени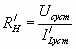е , где 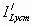- измененный ток нагрузки. Найдя из графика значение σ, по отношению 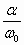определим значение: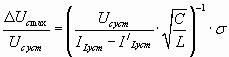

и затем находим 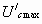. На холостом ходу 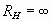и 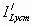=0; для идеального выпрямителя R_b = 0, отношение 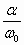=0, и тогда, преобразуя выражение, получим: 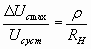где 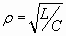- волновое сопротивление контура. Волновое сопротивление ρ контура фильтра практически всегда меньше сопротивления нагрузки 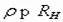, поэтому напряжение на конденсаторе при “сбросе” нагрузки (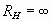) будет . Для уменьшения возникающих перенапряжений последовательно с конденсатором фильтра можно включить резистор небольшого сопротивления (десятки Ом). Рассмотрим переходный процесс при “сбросе” и “набросе” тока нагрузки (смотрите ниже рисунок). При “сбросе” тока нагрузки возникает перенапряжение, которое может привести к выходу из строя аппаратуры, поэтому при расчете LC-фильтра, необходимо учитывать режим работы на импульсную нагрузку.

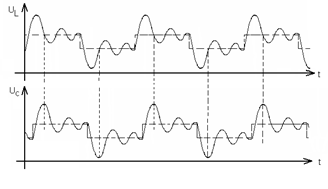
27)Что представляет собой угловая частота w_св в случае колебательного характера переходного процесса? Как она определяется расчётным путём и по осциллограмме?

Ответ: Как отмечалось в предыдущей лекции, линейная цепь охвачена единым переходным процессом. Поэтому в рассматриваемых цепях с одним накопителем энергии (катушкой индуктивности или конденсатором) – цепях первого порядка – постоянная времени будет одной и той же для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Общий подход к расчету переходных процессов в таких цепях основан на применении теоремы об активном двухполюснике: ветвь, содержащую накопитель, выделяют из цепи, а оставшуюся часть схемы рассматривают как активный двухполюсник А (эквивалентный генератор) (см. рис.1, а) со схемой замещения на рис. 1,б.

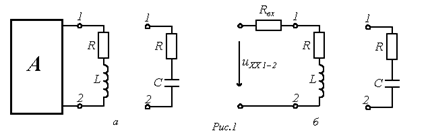
Совершенно очевидно, что постоянная времени здесь для цепей с индуктивным элементом определяется, как: 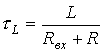, и с емкостным, как: 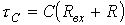, где 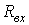- входное сопротивление цепи по отношению к зажимам 1-2 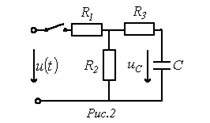подключения ветви, содержащей накопитель энергии. Например, для напряжения на конденсаторе в цепи на рис. 2 можно записать:

,

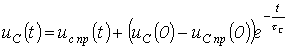где в соответствии с вышесказанным:

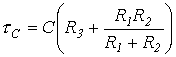. Переходные процессы при подключении последовательной
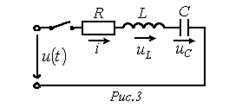R-L-C-цепи к источнику напряжения:

Рассмотрим два случая: а) 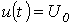; б) 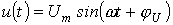. Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать

.

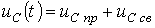(1)

Тогда для первого случая принужденная составляющая этого напряжения:

.

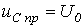(2)

Характеристическое уравнение цепи:

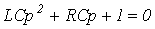, решая которое, получаем: .

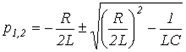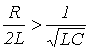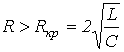В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей: 1. или , где 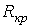- критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер. В этом случае:

.

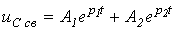(3)

2. 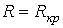- предельный случай апериодического режима. В этом случае 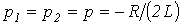и

.

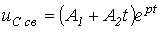(4)

3. 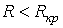- периодический (колебательный) характер переходного процесса.

В этом случае 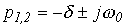и

,

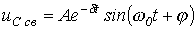(5)

где 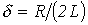- коэффициент затухания; 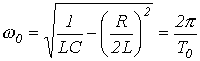- угловая частота собственных колебаний; 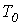- период собственных колебаний. Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать:

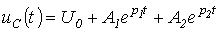. Для нахождения постоянных интегрирования, учитывая, что в общем случае 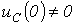и в соответствии с первым законом коммутации 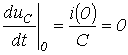, запишем для t=0 два уравнения: 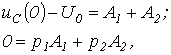решая которые, получим: 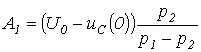; 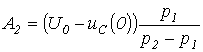. Таким образом,

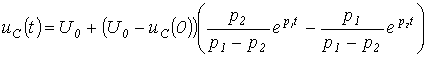. Тогда ток в цепи:

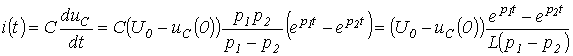
и напряжение на катушке индуктивности:

.

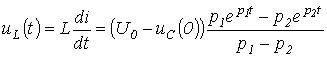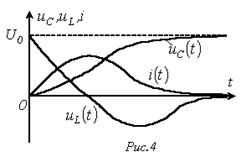На рис. 4 представлены качественные кривые 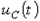, 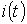и 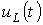, соответствующие апериодическому переходному процессу при 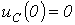. Для критического режима на основании (2) и (4) можно записать:

.

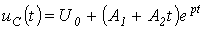При 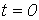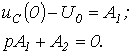Таким образом: 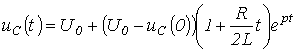и

.

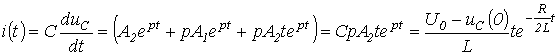Для колебательного переходного процесса в соответствии с (2) и (5) имеем: 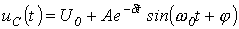. Для нахождения постоянных интегрирования запишем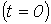 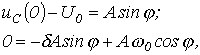откуда 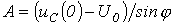и 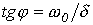. Тогда

.

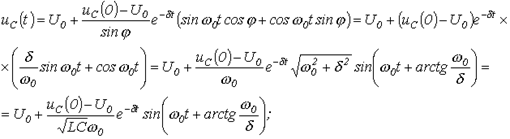
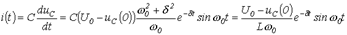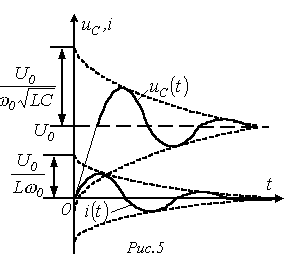На рис. 5представлены качественные кривые 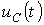и 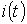, соответствующие колебательному переходному процессу при 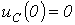. При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым:

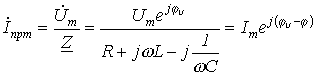
И 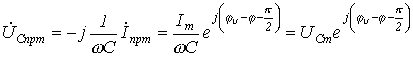, где ; ; .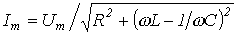

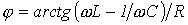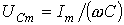Таким образом, 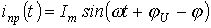и 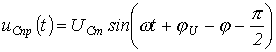. Здесь также возможны три режима:

1. 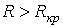;	2.	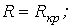3.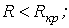

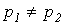
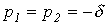
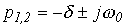
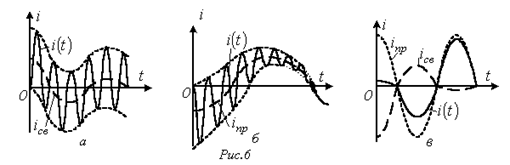
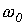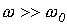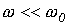Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой . При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: 1 - ; 2 - ; 3 - 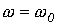, - которые представлены на рис. 6,а…6,в соответственно.