2015-05-20
6050
Для чего такое сравнение применяется? Предположим, существуют две большие группы людей (скажем, жители Москвы и Санкт-Петербурга). Требуется проверить, одинакова ли в этих группах величина некоторого параметра, измеряемого по интервальной шкале (например, одинакова ли зарплата москвичей и петербуржцев).
Очевидно, что если взять произвольного москвича и произвольного петербуржца, то их зарплаты вряд ли совпадут. Проверяется равенство средних значений параметров в группах. Иными словами: если мы опросим всех жителей Москвы и Санкт-Петербурга, то совпадут ли средние значения зарплаты в этих городах? Понятно, что всех жителей опросить нереально. Как правило, исследователь имеет выборку из N1 представителей одной группы (скажем, жителей Москвы) и N2 представителей другой группы (жителей Петербурга). В общем случае N1 не равно N2.
Первое, с чего начинается проверка равенства средних значений – это с их вычисления (это сумма всех значений, деленная на их количество):
, 
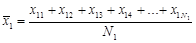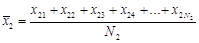
Скорее всего, вычисленные величины средних значений между собой не совпадут. Однако, различие между ними может оказаться статистически не значимым. Мы ведь опросили не всех жителей Москвы и Петербурга, поэтому в другой раз, опросив других людей, мы можем и не получить такой значительной разности средних значений, а возможно, эта разность даже поменяет знак. Значит, надо оценить, насколько разность средних значений велика по сравнению с разбросом значений в группах. Схематически это можно представить на таком рисунке:
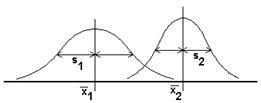
Вслед за средними значениями требуется вычислить стандартные отклонения в каждой группе – именно они служат мерой разброса. Формулы для их вычисления уже приводились:
, 
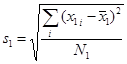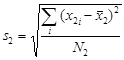
Итак, после первого этапа мы должны иметь значения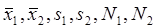 
.
Теперь формулируем гипотезу: «Средние значения в группах равны». В нашем примере эта гипотеза принимает вид «Средний доход жителей Москвы равен среднему доходу жителей Санкт-Петербурга». Математически гипотезу можно записать примерно так: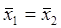 
(но под 
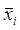в такой записи надо понимать средние параметры по популяции, а не их оценочные значения по выборкам). Альтернативную гипотезу сформулируем следующим образом: «Средние значения в группах не равны».
В случае, если гипотеза верна, разность полученных в эксперименте средних значений в двух группах обусловлена только статистическим разбросом. Чем больше разность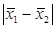 
, тем с меньшей вероятностью мы будем ее наблюдать. Осталось оценить вероятность возникновения той разности, которая была измерена в нашем эксперименте. Если эта вероятность окажется достаточно малой, то мы сделаем вывод, что только статистическим разбросом эту разность объяснить не удается, поэтому средние значения в группах не будут равны (т.е. мы отвергнем проверяемую гипотезу).
Для оценки используется следующая величина: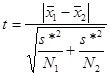 
Здесь 
s* - усредненное значение стандартного отклонения, вычисляемое по формуле: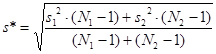 
Математики определили, что в случае, если средние значения в популяции равны, величина t (случайная величина!) имеет распределение Стьюдента с числом степеней свободы, равным d=N1+N2-2. То есть, мы знаем вид распределения t-величины, а значит, функцию и плотность этого распределения.
С практической точки зрения функция распределения дает возможность по значению t-величины определить вероятность того, что данная (или большая данной) величина t будет наблюдаться (благодаря статистическому разбросу), если на самом деле в популяции средние значения равны. Эта вероятность, как ранее уже говорилось, называется уровнем значимости и обозначается буквой α. Как правило, зависимость t от α смотрят по таблице (см. Приложение 3), выглядящей примерно так:
| Степени свободы | Значения α | ||||
| 0.01 | 0.05 | 0.02 | 0.01 | 0.001 | |
| 6,31 | 12,7 | 31,82 | 63,7 | ||
| 2,92 | 4,30 | 6,94 | 9,92 | 31,6 | |
| 2,35 | 3,18 | 4,54 | 5,84 | 12,9 | |
| 2,13 | 2,78 | 3,75 | 4,60 | 8,61 | |
| 2,01 | 2,57 | 3,37 | 4,03 | 6,86 | |
| ….. | … | … | … | … | … |
В ячейках стоят значения t-величины. Предположим, мы получили t=4 в эксперименте с тремя наблюдениями в 1-й группе и 4-мя наблюдениями во 2-й группе. Тогда сначала мы должны найти число степеней свободы (d=3+4-2=5), затем в 5-й строчке найти величину t, близкую к нашей (t=4.03) и посмотреть, колонке с каким уровнем α это соответствует. Получаем α=0,01.
Смысл полученного значения таков. Если мы проведем очень много подобных экспериментов, а средние значения на самом деле равны, то значения t-величины, большие или равные 4, мы будем получать с вероятностью 0,01, т.е. в 1% экспериментов, или в одном эксперименте из ста. То есть, мы вряд ли получили бы такую большую разность средних значений только благодаря статистическому разбросу. Поэтому гипотезу о равенстве средних значений мы отвергаем и считаем, что средние значения НЕ равны. Если бы α было порядка 0.5, это бы означало, что такие, как наблюдаемые, значения t мы получали бы в каждом втором эксперименте. И мы бы приняли гипотезу о равенстве средних значений.
Часто (ввиду ограниченности таблиц) гипотезу о равенстве средних значений проверяют в обратной последовательности:
1)Сначала выбирают уровень значимости, менее которого мы гипотезу отвергаем. Например, выбирают α=0,05, соответствующий наблюдению наших значений t в 1-м случае из 20.
2)По этому α, зная число степеней свободы, мы находим по таблице критическое значение t-величины. Например, по α=0,05 в эксперименте с 4 степенями свободы мы нашли бы tкрит=2,78.
3)Сравниваем tкрит с полученным в нашем эксперименте значением. Если наше экспериментальное значение превышает критическое, т.е. tэксп>tкрит, то мы отвергаем гипотезу, т.е. средние значения НЕ равны.
ПРИМЕР ПРОВЕРКИ РАВЕНСТВА СРЕДНИХ ЗНАЧЕНИЙ ПРИЗНАКА В ДВУХ ГРУППАХ.
Пусть требуется проверить, отличается или нет средний возраст женатых людей от среднего возраста холостых. Понятно, что речь идет о средних показателях по некоторой популяции (например, жителей города Тьмутараканска).
У нас имеется выборка из опроса жителей Тьмутараканска следующего вида:
Возраста женатых людей: 30, 28, 19, 19, 23, 19, 27, 24, 26, 20, 26 и 21 лет.
Возраста холостых: 29, 30, 21, 41, 32, 33, 18, 21, 18, 31, 27, 20 и 19 лет.
Проверяем нулевую гипотезу: «Средний возраст женатых жителей Тьмутараканска равен среднему возрасту холостых жителей Тьмутараканска». Для этого:
1) Считаем число респондентов в каждой группе: N1=12, N2=13
2) Теперь находим значения среднего возраста:
, 
.
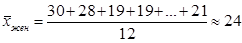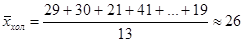3) Далее вычисляем дисперсии:
,
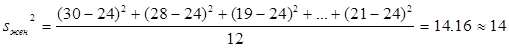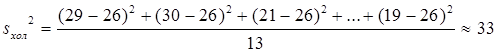
4) Находим усредненную дисперсию:
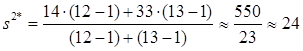
5) Вычисляем t-величину:
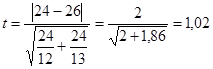
6) Определяем число степеней свободы: d=13+12-2=25-2=23.
7) Выбираем уровень значимости, начиная с которого гипотеза будет отвергнута. Например, возьмем α=0,05. По таблице для d=23 и α=0,05 находим tкрит.=2,07.
8) Сравниваем экспериментальное значение tэксп=1,02 с критическим значением tкрит.=2,07. Поскольку tэксп<tкрит., мы не отвергаем нулевую гипотезу и считаем, что средние значения возраста женатых и холостых жителей Тьмутараканска равны.
Осталось сделать одно замечание. Применять формулу для t=величины, в которую входит усредненное значение дисперсии возможно, только если дисперсии в группах примерно равны, либо достаточно велики значения N1 и N2. Если это не так, то возможны неточности, связанные с тем, что распределение t-величины будет отличаться от t-распределения Стьюдента.
Иногда данные могут быть представлены в виде ответа на два вопроса (т.е. двух признаков), одним из которых является измеряемое по интервальной шкале значение некоторой величины, по которой можно вычислять средние значения (например, возраст), а другим – признак группы (номинальная шкала, например, семейное положение). Эти два столбца нетрудно переписать в виде двух групп значений возраста, после чего применять только что описанный метод.
