В том случае, когда заправка осуществляется подвижными агрегатами обслуживания, работа такой системы заправки может быть смоделирована замкнутой системой массового обслуживания, в которой число источников заявок N ограничено количеством обслуживаемых ЛА, а интенсивность поступления заявок формула зависит от состояний источников, обусловленных работой самой системы. Такая задача обычно решается в следующей постановке. Имеется N одинаковых, взаимно удаленных объектов, каждый из которых может в некоторое случайные моменты времени подать заявку на обслуживание. Поток заявок каждого объекта считается Пуассоновским с интенсивностью формула. Каждый объект может обслуживаться одним (нет взаимопомощи между каналами) или формула (имеется частичная взаимопомощь) агрегатами обслуживания. Интенсивность пуассоновского потока обслуживаний каждого канала формула. Если к моменту подачи заявки объектом все каналы заняты, то этот объект становиться в очередь на обслуживание; дисциплина очереди такая: кто раньше подал заявку, тот раньше обслуживается.
Для случая отсутствия взаимопомощи между каналами обслуживания состояние замкнутой системы массового обслуживания описывается системой дифференциальных уравнений:
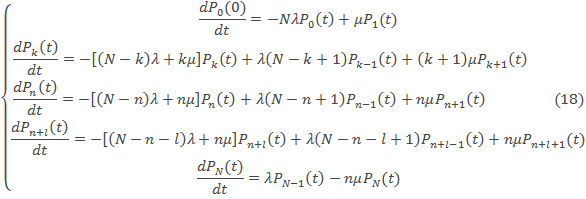
Решение системы дифференциальных уравнений (18) совместно с нормировочным условием
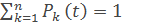 (19)
(19)
позволяет определить все вероятные состояния замкнутой системы массового обслуживания и найти все параметры, характеризующие работу этой системы в режиме постановки ЛА на работу.
Для стационарного режима работы подвижных агрегатов обслуживания система (18) превращается в систему алгебраических уравнений:
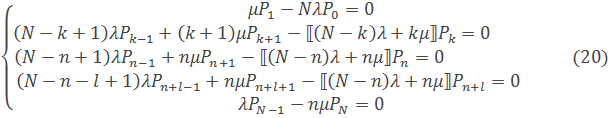
Решение этой системы уравнений совместно с нормировочным условием (19) дает следующие выражения для определения вероятностей нахождения в состояниях 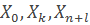 :
:
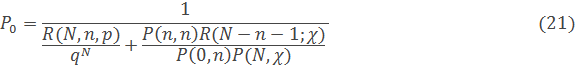
 (22)
(22)
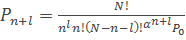 (23)
(23)
Где k=1,2,3,…,n; 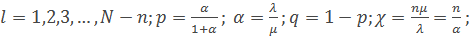
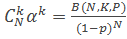 – вычисляется по таблицам биноминального распределения;
– вычисляется по таблицам биноминального распределения;
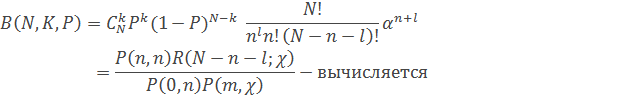
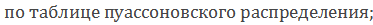
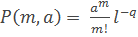
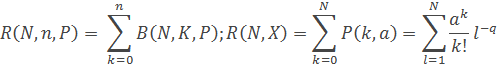
Таблицы биноминального и пуассоновского распределений всех указанных выше функций приведены в ____.
Зная вероятные состояния системы массового обслуживания замкнутого типа, легко определить и другие параметры, характеризующие процесс функционирования системы и заявка объекта – обслуживание агрегатом. Так среднее число обслуживаемых объектов 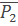 определяется по формуле:
определяется по формуле: 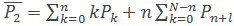 (24)
(24)
Среднее число ожидаемых очереди объектов формула, можно найти так:
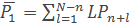 (25)
(25)
Среднее число простаивающих объектов: 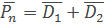 (26)
(26)
Коэффициент использования 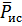 (вероятность того, что определенный объект в любой момент времени будет работать и не нуждаться в обслуживании) подсчитывают по формуле:
(вероятность того, что определенный объект в любой момент времени будет работать и не нуждаться в обслуживании) подсчитывают по формуле:
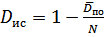 , (27)
, (27)
где 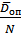 =
= 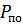 - вероятность простаивания объекта, т.е. вероятность того, что объект нуждается в обслуживании.
- вероятность простаивания объекта, т.е. вероятность того, что объект нуждается в обслуживании.
Среднее время готовности объекта к применению будет равно:
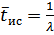 ; (28)
; (28)
Средние времена простоя объекта и пребывания его в очереди определяется выражениями:
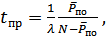 (29)
(29)
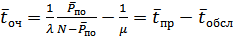 , (30)
, (30)
где 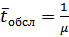 – среднее время обслуживания одного объекта одним агрегатом.
– среднее время обслуживания одного объекта одним агрегатом.
Для случая работы замкнутой системы массового обслуживания с взаимопомощью между каналами обслуживания задача определения параметров функционирования формулируется следующим образом: имеется N одинаковых взаимно удаленных объектов, каждый из которых в любой случайный момент времени может подать заявку на обслуживание с интенсивностью 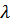 : интенсивность обслуживания каждым агрегатом равна
: интенсивность обслуживания каждым агрегатом равна 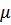 . Если подано заявок меньше
. Если подано заявок меньше 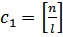 , то каждый объект обслуживаться одновременно
, то каждый объект обслуживаться одновременно 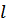 агрегатами, где
агрегатами, где 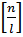 – целая часть числа
– целая часть числа 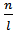 . Производительность при этом возрастает в
. Производительность при этом возрастает в 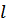 раз и равна
раз и равна 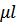 . Величина
. Величина 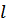 определяется максимальным числом агрегатов, которые могут быть использованы при обслуживании одного объекта. Если подано заявок
определяется максимальным числом агрегатов, которые могут быть использованы при обслуживании одного объекта. Если подано заявок 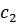 , причем
, причем 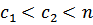 , то в обслуживании участвуют все
, то в обслуживании участвуют все 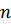 агрегатов, при этом каждый объект обслуживается не более чем
агрегатов, при этом каждый объект обслуживается не более чем 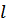 агрегатами. Если подано заявок
агрегатами. Если подано заявок 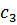 , причем
, причем 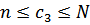 , то в обслуживании участвуют n агрегатов, которые обслуживают
, то в обслуживании участвуют n агрегатов, которые обслуживают 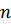 объектов, а
объектов, а 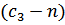 объектов ожидают очереди на обслуживание.
объектов ожидают очереди на обслуживание.
 Процесс функционирования замкнутой системы массового обслуживания с взаимопомощью между каналами обслуживания описывается системой дифференциальных уравнений:
Процесс функционирования замкнутой системы массового обслуживания с взаимопомощью между каналами обслуживания описывается системой дифференциальных уравнений:
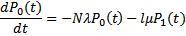
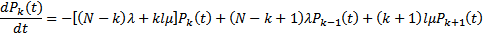
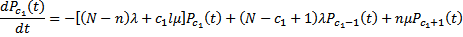
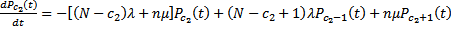 (31)
(31)
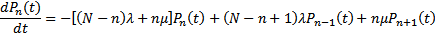
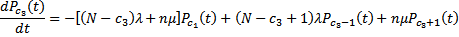
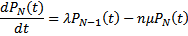
Эта система уравнений решается совместно с нормировочным условием (19) и дает возможность определить параметры, характеризующие работу заправочной системы с помощью подвижных агрегатов обслуживания в режиме постановки ЛА на работу.
Для стационарного режима работы такой системы массового обслуживания системы дифференциальных уравнений (31) преобразуются к виду:
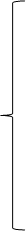
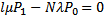
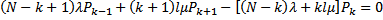
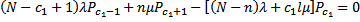
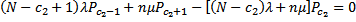 (32)
(32)
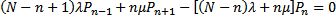
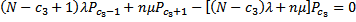
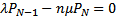
В результате решения системы алгебраических уравнений (32) совместно с условием (19) получаются следующие выражения для определения вероятных состояний подобной системы массового обслуживания:
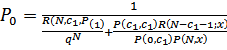 (33)
(33)
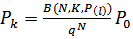
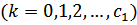 (34)
(34)
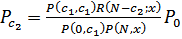
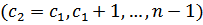 (35)
(35)
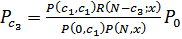
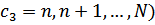 (36)
(36)
где 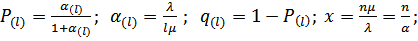
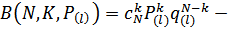 табличная функция биноминального распределения.
табличная функция биноминального распределения.
 2015-05-10
2015-05-10 383
383








