2015-05-10
439
Выше указывалось, что процесс заправки ЛА через централизованную заправочную систему представляет собой последовательное изменение числа подготавливаемых к заправке, находящих одновременно под заправкой ЛА и аппаратов, на которых проводятся после заправочные операции, и что система обслуживания ЛА через ЦЗС может быть отнесена к системе массового обслуживания разомкнутого типа с неограниченным ожиданием.
Определение параметров, характеризующих процесс обслуживания ЛА в этом случае, осуществляется путем исследования n – канальной системы массового обслуживания, на вход которой поступает простейший поток заявок с интенсивностью формула и интенсивностью обслуживания каждого канала формула: если поступившая заявка застанет свободным хотя бы один канал, она немедленно принимается за обслуживание и обслуживается до конца, в противном случае заявка попадает в очередь с количеством мест в очереди m. Очевидно, что m=0 получается система массового обслуживания с отказами, а при формула – система с ожиданием. Каждая заявка может обслуживаться либо одним каналом – нет взаимопомощи между каналами – либо несколькими свободными каналами – есть взаимопомощь между каналами.
Для случая, когда отсутствует взаимопомощь между каналами обслуживания, состояние системы массового обслуживания разомкнутого типа описывается с помощью системы дифференциальных уравнений
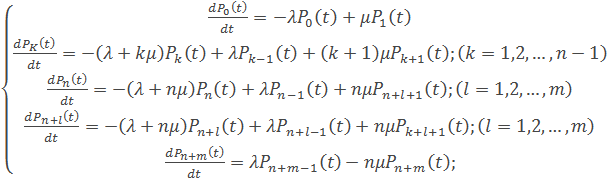(1)
где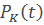 
- вероятность, что в момент времени t система будет находиться в состоянии 
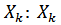- в системе k заявок, и они обслуживаются k каналами, очереди нет; 
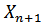- в системе имеется n+l заявок, причем n из них обслуживается и l заявок находится в очереди.
Интегрирование этой системы дифференциальных уравнений совместно с нормировочным условием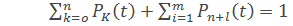 
(2)
позволяет найти все вероятные состояния системы массового обслуживания в произвольный момент времени в процессе выхода системы на стационарный режим, т.е. в процессе постановки ЛА на работу.
При стационарном режиме работы рассматриваемой системы массового обслуживания системы уравнений (1) превращается в систему алгебраических уравнений вида:
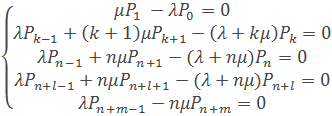(3)
Которая решается совместно с нормировочным условием (2) и дает следующие зависимости для определения вероятностей нахождением системы в состояниях формула.
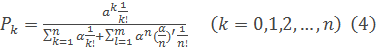
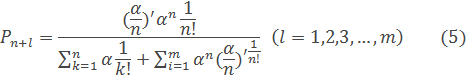
Здесь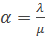 
– среднее число заявок, поступающих в рассматриваемую систему за среднее время обслуживания одной заявки одним каналом.
Зная вероятные состояния системы в любой момент времени, легко определить все параметры, характеризующие работу системы массового обслуживания.
Так, вероятность обслуживания определяется вероятностью того, что к моменту поступления ее на обслуживание, будет свободен хотя бы один канал или одно место в очереди:
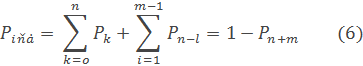
Где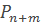 
– определяется по формуле (5).
Далее может быть определено среднее число занятых каналов:
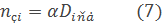
Вероятность занятости любого канала в произвольный момент времени определяется по формуле:
Где n-количество каналов обслуживания;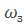 
– среднее число заявок, поступавших в систему за среднее время обслуживания всеми каналами.
Вероятность того, что система полностью загружена, равна вероятности того, что в системе заняты все каналы:
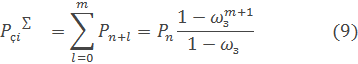
Среднее время неполной загрузки определяется из выражения
Где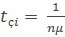 
– - среднее время полной загрузки системы.
Среднее число заявок, находящихся в очереди равно
Среднее время ожидания заявок в очереди
Среднее время нахождения заявки в системе складывается из средних времен ожидания и обслуживания, т.е.
Таким образом, определены основные параметры, характеризующие качество работы централизованной системы заправки при отсутствии взаимопомощи между каналами обслуживания.
В том случае, когда существует взаимопомощь между каналами обслуживания, состояние системы массового обслуживания описывается с помощью системы дифференциальных уравнений вида:
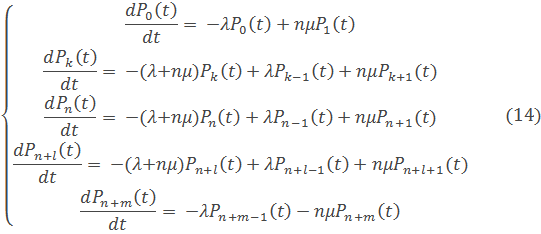
В стационарном состоянии, которая превращается в системы алгебраических уравнений:
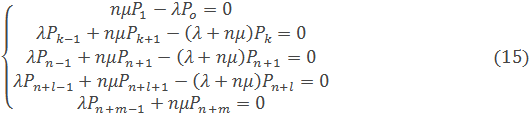
Параметры, характеризующие работу такой системы массового обслуживания, определяются выражениями аналогичными (6-13), в которых вероятности нахождения системы в состояниях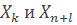 
находятся путем интегрирования системы уравнений (14). Cсовместно с нормировочным условием (12) для случая постановки ЛА на дежурство и путем решения системы уравнений (1) и (2) для стационарного режима работы централизованной заправочной системы с взаимопомощью между агрегатами обслуживания. В частности, для стационарного режима работы вероятность пребывания системы в j-ом состоянии (j = 0,1,2,3...,k,...,n,...,n+l,..., n+m)находится из выражения:
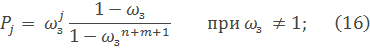
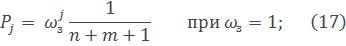
Где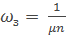 
– - среднее число заявок, поступающих в систему за среднее время обслуживания всеми каналами.
