Лабораторная работа №3. Логические операции, равносильность формул.
Цель работы. Изучить логические операции и основные равносильности алгебры логики, научиться составлять таблицы истинности для формул алгебры логики и преобразовывать формулы, используя основные равносильности и правила поглощения.
Задание 1. Построить таблицы истинности для высказываний
1) 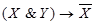 ; 2)
; 2) 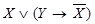 ; 3)
; 3) 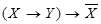 ; 4)
; 4) 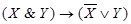 ;
;
5) 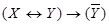 ; 6)
; 6) 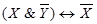 ; 7)
; 7) 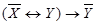 ; 8)
; 8) 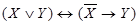 ;
;
9) 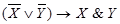 ; 10)
; 10) 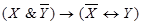 .
.
Пример. Построить таблицу истинности для высказывания 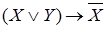
| X | Y | XÚY | 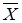 | 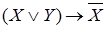 |
Задание 2. Используя основные равносильности алгебры логики, доказать равносильность формул:
1) 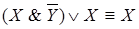 ; 2)
; 2) 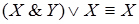 ; 3)
; 3) 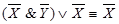 ;
;
4) 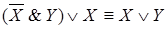 ; 5)
; 5) 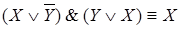 ;
;
6) 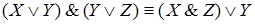 .
.
Основные равносильности алгебры логики:
2. A&B≡B&A — коммутативный закон для конъюнкции
3. AÚB≡BÚA — коммутативный закон для дизъюнкции
4. (A&B)&C≡A&(B&C) — ассоциативный закон для конъюнкции
5. (AÚB)ÚC≡AÚ(BÚC) — ассоциативный закон для дизъюнкции
6. A&(BÚC) ≡ (A&B)Ú(A&C) — дистрибутивные законы
7. AÚ (B&C) ≡ (AÚB)&(AÚC)
8. A&A≡A — закон идемпотентности для конъюнкции
9. AÚA≡A — закон идемпотентности для дизъюнкции
10. 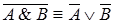 — закон де Моргана
— закон де Моргана
11. 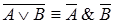 — закон де Моргана
— закон де Моргана
12. A&1≡A — закон единицы для конъюнкции
13. A&0≡0 — закон нуля для конъюнкции
14. AÚ1≡1 — закон единицы для дизъюнкции
15. AÚ0≡A — закон нуля для дизъюнкции
Пример. Доказать, что 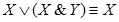 .
.
Решение. Закон единицы для конъюнкции позволяет заменить Х на X&1:
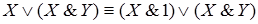 .
.
Используя дистрибутивный закон, вынесем Х за скобки:
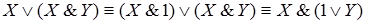 .
.
Закон единицы для дизъюнкции гласит 1ÚYº1, а закон единицы для дизъюнкции Х&1ºХ позволяет получить искомое выражение:
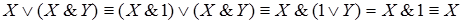 , что требовалось доказать.
, что требовалось доказать.
Задание 3. Используя основные равносильности алгебры логики, а также равносильности упростить формулы:
1) 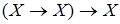 ; 2)
; 2) 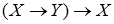 ; 3)
; 3) 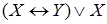 ; 4)
; 4) 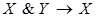 ;
;
5) 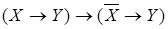 ; 6)
; 6) 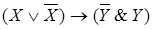 ; 7)
; 7) 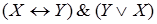 ;
;
8) 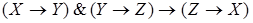 ;
;
9) 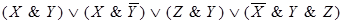 .
.
 2015-05-10
2015-05-10 746
746
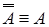 —
— 






