2015-05-10
335
Модуль 5
Решение иженерных задач средствами
Компьютерной математики
Лабораторная работа № 4
Нахождение производных и интегралов
Цель: изучить основные возможности приложения Smath Studio для нахождения производных и интегралов.
Вопросы для самоконтроля
1. На какой ПИ находятся шаблоны для нахождения производной и определенного интеграла?
2. Стандартные функции для нахождения производной и определенного интеграла?
Индивидуальные задания
1. Найти значение первой производной функции f(x) (табл.1) в точке x.
2. Найти аналитическое выражение для производной порядка n этой функции.
3. Найти определённый интеграл функции f(x) на отрезке [a,b] (табл.2).
Таблица 1
| № варианта | f(x) | x | n | № варианта | f(x) | x | n |
| 
| ||||||
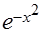
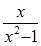
| Sin2x | x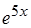 
| ||||||
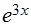
| Ln3x | ||||||
| 
| ||||||
| 
| ||||||
| 
| ||||||
| 
| ||||||
| 
| ||||||
|
| 
| ||||||
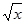
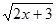
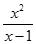
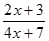
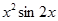
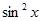
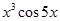
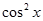
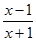
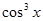
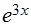
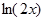
| x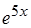
| 
| ||||||
|
|
| ||||||
|
|
| ||||||
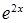
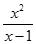
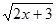
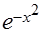
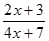
| x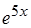
|
Таблица 2.2.6
|
|
|
| № варианта | f(x) | a | b | № варианта | f(x) | a | b |
| 
| ||||||
| 
| ||||||
| 
| ||||||
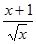
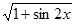
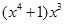
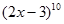
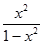
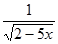
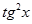
| -1 |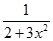 
| -1 | ||||
| 
| ||||||
| 
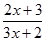
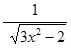
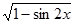
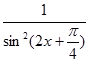
| 1,5 | 2,7 | ||||
| 
| ||||||
| 
| ||||||
| 
|
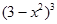
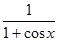
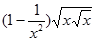
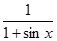
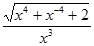
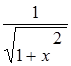
Продолжение таблицы 2.2.6
| № варианта | f(x) | a | b | № варианта | f(x) | a | b |
| 
| ||||||
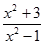
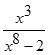
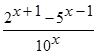
| -2 | -1 |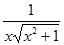 
| ||||
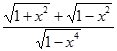
| -3 | -1 |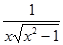 
| ||||
|
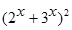
Пример выполнения задания
1) найти значение первой производной функции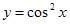 
в точке x=6.
2) найти аналитическое выражение для производной порядка n=3 этой функции.
3) найти определённый интеграл функции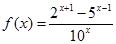 
на отрезке [2, 5].
