Выбор уравнения регрессии

Как в парном, так и во множественном регрессионном анализе используются линейные и нелинейные уравнения регрессии. Наиболее широко используются линейная и степенная функция, поскольку они имеют четкую интерпретацию параметров.

В линейной множественной регрессии 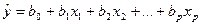параметры при 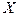называются коэффициентами «чистой регрессии». Коэффициенты «чистой регрессии» характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне. Свободный член 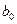не подлежит экономической интерпретации. Его роль сводится к тому, что он вбирает в себя информацию о прочих не учитываемых в модели факторах. Формально его значение предполагает то значение объясняемой переменной, когда все 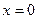, что практически не бывает.

Пример. Зависимость расходов на продукты питания по совокупности семей характеризуется следующим уравнением: 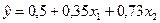, здесь 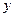– расходы семьи за месяц на питание; 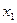– месячный доход на 1 члена семьи; 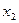– размер семьи, человек. Из данного уравнения следует, что если размер семьи увеличится на одного человека, то расходы на питание увеличится на 730 руб., когда ежемесячный доход семьи в расчете на одного человека остается постоянным. Кроме того, если доходы увеличатся на 1000 руб. на одного члена семьи, то расходы на питание увеличатся на 350 руб.

Функция потребления 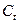имеет вид 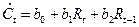, то есть потребление в момент времени 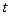зависит от дохода того же периода 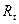и от дохода предшествующего периода 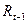. Здесь 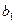– краткосрочная предельная срочность к потреблению; 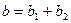– долгосрочная склонность к потреблению.

Функция потребления может рассматриваться в зависимости от прошлых привычек потребления: 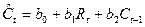. Здесь 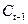– предыдущий уровень потребления. Долгосрочная предельная склонность к потреблению вычисляется по формуле: .

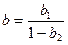В степенной функции 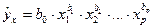коэффициенты 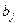являются коэффициентами эластичности. Коэффициенты эластичности показывают на сколько процентов в среднем изменяется результат с изменением соответствующего фактора на 1 % при неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и предложения.