Лабораторная работа № 5
Анализ линейных устройств в программной среде "Mathcad"
Цель работы
Изучить методы временного и спектрального анализа линейных устройств в среде "Mathcad" и получить навыки их использования.
Подготовка к работе
По [1] изучить материал страниц 40-49
[1] – В.И.Каганов. Радиотехника плюс компьютер плюс Mathcad М.2001
Пояснения к работе
Анализ линейных устройств сводится к расчету двух видов характеристик – временных и частотных.
Основой временного исследования является прямое и обратное преобразование Лапласа, спектрального – прямое и обратное преобразование Фурье. Согласно преобразованию Лапласа определяется передаточная функция устройства 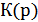 , позволяющая найти временные характеристики. Согласно преобразованию Фурье определяется коэффициент передачи
, позволяющая найти временные характеристики. Согласно преобразованию Фурье определяется коэффициент передачи 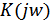 , определяющий частотные свойства объекта.
, определяющий частотные свойства объекта.
Поскольку интегралы Фурье являются частным случаем преобразования Лапласа, то между 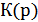 и
и 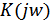 существует прямая связь, позволяющая от временных характеристик перейти к частотным и обратно
существует прямая связь, позволяющая от временных характеристик перейти к частотным и обратно
Передаточная функция линейного устройства может быть представлена в виде:
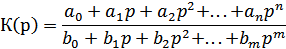
или при разложении числителя и знаменателя на множители (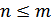 ):
):
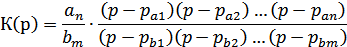
где 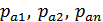 – корни уравнения
– корни уравнения
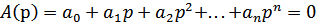
называемые нулями передаточной функции 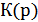 ;
;
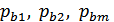 – корни уравнения
– корни уравнения
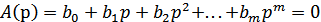
называемые полюсами передаточной функции 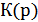 .
.
В устойчивой системе все полюсы оператора 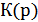 располагаются в левой полуплоскости комплексного переменного
располагаются в левой полуплоскости комплексного переменного 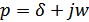 , т.е. действительные части всех полюсов
, т.е. действительные части всех полюсов 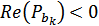 , где
, где 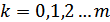
Коэффициент передачи 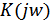 можно представить в виде
можно представить в виде
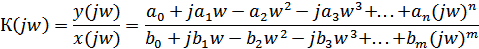
Это выражение можно представить в виде
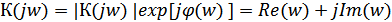
где модуль и фазу коэффициента передачи можно выразить через действительную и мнимую части комплексною числа
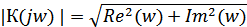
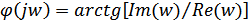
С помощью приведенных выше выражений можно определить частотные и временные характеристики линейного устройства.
Амплитудно-частотная характеристика (АЧХ) есть модуль комплексного коэффициента передачи:
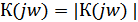 .
.
Фазо-частотная характеристика (ФЧХ) есть аргумент комплексного коэффициента передачи:
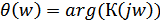 .
.
Переходную характеристику 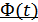 можно выразить через действительную часть коэффициента передачи:
можно выразить через действительную часть коэффициента передачи:
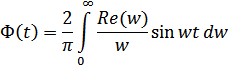
Импульсная характеристика 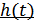 может быть определена также по действительной части коэффициента передачи:
может быть определена также по действительной части коэффициента передачи:
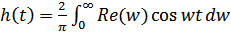 .
.
 2015-05-10
2015-05-10 330
330







