Математический аппарат описания динамики систем управления

Лабораторная работа №3

Тема: Изучение типовых звеньев систем управления.

Цель работы: Изучение временных и частотных характеристик основных типов динамических звеньев (апериодическое звено 1-го порядка и колебательное звено); освоение способа экспериментального определения неизвестных параметров этих звеньев по их временным характеристикам с помощью MaTHlab.

Содержание работы:

1. Создание моделей динамических звеньев 1-го и 2-го порядков с помощью пакета расширения Simulink и снятие их экспериментальных характеристик (переходной и весовой функций, частотных амплитудной и фазовой, логарифмических амплитудной и фазовой).

2. Проверка полученных значений с помощью пакета расширения Control System Toolbox и сравнение результатов моделирования.

Основные теоретические сведения

Математический аппарат описания динамики систем управления

Дифференциальные уравнения. Чтобы составить уравнения динамики системы автоматического управления или регулирования, система разбивается на звенья. Затем рассматривается каждое звено системы в отдельности: Входная g и выходная y величины соответствуют физическим величинам, выражающим воздействие предыдущего звена на данное звено (g) и воздействие данного звена на последующее (y).

Звено системы может являться техническим устройством любой физической природы, конструкции и назначения. Поэтому составление уравнения динамики каждого конкретного звена системы является предметом соответствующей конкретной области технических наук (электротехники, теплотехники, динамики полета и т.п.), к которым и следует каждый раз обращаться.

Допустим, что в результате составления уравнения динамики какого-нибудь конкретного звена получилось следующее линейное дифференциальное уравнение второго порядка:

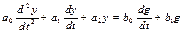
В теории автоматического регулирования принято приводить уравнение звена к стандартному виду в символической записи

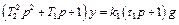, (1)

где р обозначает операцию дифференцирования 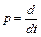, введенные постоянные времени равны 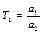, , 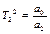, 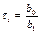а коэффициент усиления (передаточное число) звена есть

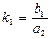
Очевидны следующие размерности этих постоянных:

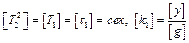
В установившемся состоянии, когда g = const и y = const из (1) получаем уравнение статики данного звена

y = k ₁ g

Коэффициент усиления k ₁, определяет крутизну наклона соответствующей линейной статической характеристики звена

k ₁= tg α,

где α – угол наклона характеристики к оси Оg.

Передаточная функция звена. Ее определение дается на базе преобразования Лапласа:

, .

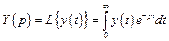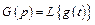Пусть даны начальные условия:

, , .

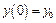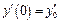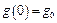Тогда:

, , .

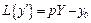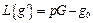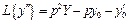Применив это преобразование, например, к дифференциальному уравнению звена (1) получим:

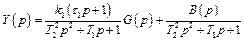(2)

где через B (p) обозначим многочлен, включающий в. себя все члены с величинами начальных условий.

Передаточной функцией звена W (p) называется отношение изображения Лапласа выходной величины к входной:

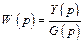
при нулевых начальных условиях (B (p)=0). В данном случае согласно (2) имеем

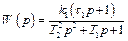(3)

Сравнивая полученное выражение с дифференциальным уравнением звена (1), видим, что формально передаточную функцию звена можно составлять как отношение операторных многочленов правой и левой частей уравнения звена. И наоборот, зная передаточную функцию (3), легко написать его уравнение, имея в виду, что числитель передаточной функции соответствует правой части уравнения (1), а знаменатель передаточной функции (3) – левой части уравнения (1).

В общем случае передаточная функция звена имеет вид

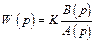(4)

где B (p) и A (p) - многочлены с коэффициентами 1 в младших членах, причем степень B (p), как правило, ниже степени A (p).

Переходная функция звена. Переходной функцией h (t) называется реакция звена на ступенчатое единичное воздействие, т.е. переходный процесс на выходе Х ₂ при единичном скачке 1 (t) на входе звена x ₁. Следовательно,

, ,

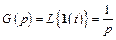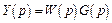откуда

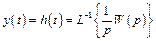
Весовая функция звена. Весовой функцией звена называется оригинал (т.е. обратное преобразование Лапласа) передаточной функции

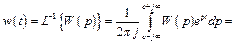
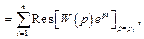
где p_i, – все полюса передаточной функции W (p). В этой формуле Res обозначает вычеты (см. теорию функций комплексного переменного).

Поскольку при нулевых начальных условиях и G = 1, т.е. если 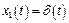–дельта-функция, то будет иметь место равенство

.

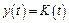Следовательно, физический смысл весовой функции звена w (t) есть реакция звена на единичный импульс, длительность которого стремится к нулю, а амплитуда к бесконечности, причем их произведение равно 1.

Иначе говоря, весовая функция представляет переходный процесс на выходе звена при подаче на его вход единичного импульса.

Поскольку известно, что (имея в виду обобщенные функции)

,

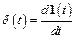то имеем следующее соотношение между весовой и переходной функциями

.

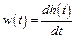Зная весовую функцию звена w (t), можно определить его передаточную функцию:

W (p)= L { w (t)}.

Частотные характеристики звена. К ним относятся:

– частотная передаточная функция (комплексный коэффициент передачи):

,

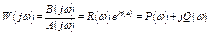а также ее вещественная 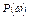и мнимая 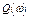составляющие;

– амплитудная и фазовая частотные характеристики

, ;

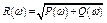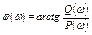– логарифмическая амплитудная частотная характеристика

.

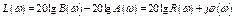Достоинством последней характеристики является то, что она представляет частотную характеристику любой системы последовательностью асимптот с углом наклона, кратным 20 дБ/дек.