1. Если дуга некоторой кривой 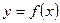 ,
, 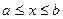 вращается вокруг оси Ох, то получится некоторая поверхность вращения, площадь которой вычисляется по формуле:
вращается вокруг оси Ох, то получится некоторая поверхность вращения, площадь которой вычисляется по формуле:
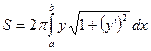 .
.
2. Если кривая, заданная параметрически 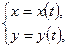 где
где 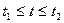 , вращается вокруг оси Ох, то площадь получающейся поверхности находится по формуле:
, вращается вокруг оси Ох, то площадь получающейся поверхности находится по формуле:
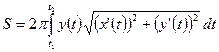 .
.
3. Если кривая, заданная в полярной системе координат уравнением 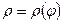 , где
, где 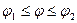 , вращается вокруг полярной оси, то площадь получающейся поверхности равна:
, вращается вокруг полярной оси, то площадь получающейся поверхности равна:
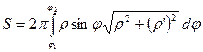 .
.
Пример 2. Найдем площадь поверхности, образованной вращением вокруг оси Ох одной арки циклоиды 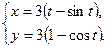
Решение. Одна арка циклоиды получается при 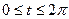 . Используя соответствующую формулу, вычисляем:
. Используя соответствующую формулу, вычисляем:
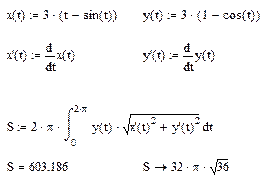
 2015-05-10
2015-05-10 1592
1592








