1. Рассмотрим криволинейную трапецию, ограниченную графиком функции 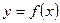 , прямыми
, прямыми 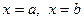 и осью Ох. Если эту трапецию вращать вокруг одной из координатных осей, то получится некоторое объёмное тело. Объём полученного тела вращения можно вычислить при помощи определённого интеграла:
и осью Ох. Если эту трапецию вращать вокруг одной из координатных осей, то получится некоторое объёмное тело. Объём полученного тела вращения можно вычислить при помощи определённого интеграла:
- если трапеция вращается вокруг оси Ох, то 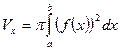 ;
;
- если трапеция вращается вокруг оси Оу, то 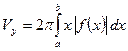 .
.
Если вращается фигура, ограниченная кривыми 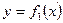 и
и 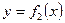
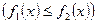 , и прямыми
, и прямыми 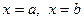 , то формулы для вычисления объёма запишутся соответственно:
, то формулы для вычисления объёма запишутся соответственно:
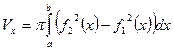 и
и 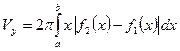 .
.
2. Если фигура, ограниченная кривой, заданной параметрически 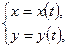 где
где 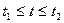 , вращается вокруг оси Ох или Оу, то объемы получающихся тел вращения вычисляются по формулам:
, вращается вокруг оси Ох или Оу, то объемы получающихся тел вращения вычисляются по формулам:
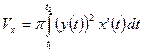 и
и 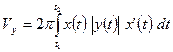 .
.
3. В полярных координатах криволинейный сектор, ограниченный кривой 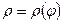 и лучами
и лучами 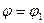 и
и 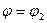 , можно вращать вокруг полярной оси. Объём получающегося тела вращения вычисляется по формуле:
, можно вращать вокруг полярной оси. Объём получающегося тела вращения вычисляется по формуле:
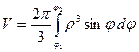 .
.
Пример 1. Найдем объём тела, образованного вращением вокруг полярной оси кардиоиды 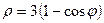 .
.
Решение. Построим кардиоиду:
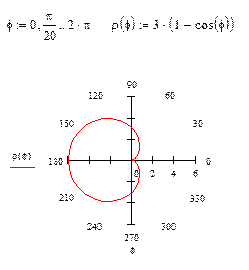
Видим, что при изменении j от 0 до 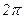 получается фигура, симметричная относительно полярной оси. Тело вращения получается при вращении вокруг полярной оси только одной её части, например, той, что расположена выше полярной оси. Поэтому интеграл вычисляем в пределах от 0 до p.
получается фигура, симметричная относительно полярной оси. Тело вращения получается при вращении вокруг полярной оси только одной её части, например, той, что расположена выше полярной оси. Поэтому интеграл вычисляем в пределах от 0 до p.
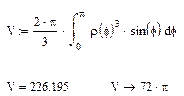
 2015-05-10
2015-05-10 8035
8035








