Интерполяция на практике хороша лишь для таких функций, значения которых не искажены шумом. Случайные ошибки в значениях функции сильно искажают интерполяционное многочлены высоких степеней, а при интерполяции многочленами низких степеней теряется существенная информация. Поэтому, в этом случае, целесообразно применять «сглаживающую» аппроксимацию с минимизацией взвешенной средней квадратической ошибки аппроксимации. Это значит, что для данной функции f(х) требуется построить функцию F(х) вида
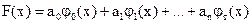 |
(16)
так, чтобы минимизировать взвешенную среднюю квадратическую ошибку на интервале [a,b]:
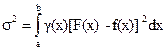 |
(17)
где g(х)– заданная весовая неотрицательная функция.
Если функции j(x) действительны и попарно ортогональны с весом g(х) на интервале [a,b], то есть если
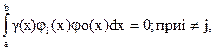 |
(18)
то искомые коэффициенты определяются по формуле
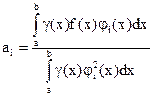 | 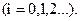 | ||
 |
(19)
Аппроксимация ортогональными функциями, например, ортогональными многочленами или тригонометрическими полиномами имеет то замечательное преимущество, что улучшение аппроксимации путем добавления нового члена an+1 jn+1 (x) не меняет ранее вычисленные коэффициенты а0, а1, а2, …,аn.
Таким образом, для аппроксимации функции f(х) необходимо задать класс приближающих функций или n- мерное пространство, где n- число заданных значений функции f(х), и норму в этом пространстве. При приближении функций многочленами на дискретном множестве точек норма имеет вид:
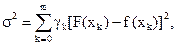 |
(20)
где gk заданные положительные веса,
m + 1 - дискретное множество точек.
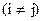 | |||
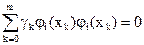 | |||
Согласно условию ортогональности (18):
(21)
и на основании (19) имеем:
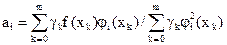 | 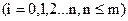 | ||
(22)
Отметим, что можно использовать другую норму (20), тогда получим другое приближение, которое может значительно отличатся от предыдущего
Приведем пример аппроксимации функций тригонометрическим многочленом:
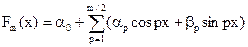 |
(23)
Коэффициенты этого многочлена при учете условия (20) находятся согласно формулам:
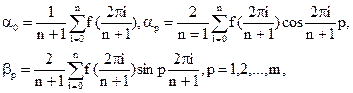 |
(24)
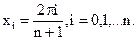 |
где
Цель работы: Получить практические навыки децимации и интерполяции сигналов
1. Запишите математическое выражение полигармонического сигнала с трендом. Нарисуйте его спектр.
2. Вычислите частоту дискретизации сигнала, полученного в п.1, и с помощью программы REEBOK создайте файл данных с этим сигналом. Вычислите спектр сигнала, записанного в полученном файле данных, и сравните его с теоретическим, полученным в п.1.
3. Составьте схему алгоритма и программный модуль для уменьшения в два раза числа отсчетов сигнала, полученного в п.1, не изменяя интервал наблюдения сигнала (апертуру).
4. Запустите программный модуль, полученный в п.3, подав на его вход сигнал, файл данных которого был получен в п.2. Зарисуйте сигнал на выходе программного модуля. Получите его спектр. Сравните его со спектром исходного сигнала.
5. Составьте схему алгоритма и программный модуль для увеличения в два раза числа отсчетов сигнала, полученного в п.1, не изменяя интервал наблюдения сигнала.
6. Запустите программный модуль, полученный в п.5, подав на его вход сигнал, файл данных которого был получен в п.2. Зарисуйте сигнал на выходе программного модуля. Получите его спектр. Сравните его со спектром исходного сигнала.
Литература
1. Методические указания к лабораторной работе "Интерполяция и аппроксимация кривых"/Курск. политехн. ин-т; Сост. С.А. Филист. Курск. КПИ.1993. 13 с.
 2015-05-10
2015-05-10 921
921








