Кинематика и динамика.

Колебания и волновые процессы

Вариант № 1

1. Тело, двигаясь с постоянным ускорением, проходит последовательно два одинаковых отрезка пути S по 10 м каждый. Найти ускорение в начале первого отрезка, если первый отрезок пройден телом за время t₁=1,06 с, а второй за t₂=2,2 с.

Ответ: а) а=3 м/с²; б) a=2 м/с²; в) a=1 м/с²; г) a=0; д) а=-3 м/с².

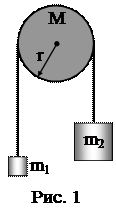
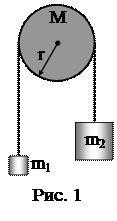
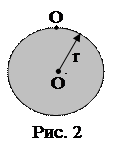
2. Две гири массами m₁=1 кг и m₂=2 кг соединены нитью, перекинутой через блок (рис. 1). Радиус блока r=0,1 м и его масса M=1 кг. Найти ускорение, с которым движутся гири. Блок считать однородным диском. Трением пренебречь.

Ответ: а) а=3,8 м/с²; б) а=2,8 м/с²;

в) а=4,8 м/с²; г) а=1,8 м/с²; д) а=0,8 м/с².

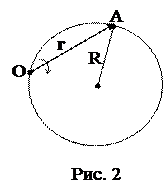
3. От бакена, который находится на середине широкой реки, отошли две лодки – А и В (рис. 2). Обе лодки движутся по взаимно перпендикулярным прямым: лодка А – вдоль реки, а лодка В – поперек. Удалившись на одинаковое расстояние от бакена, лодки вернулись затем обратно. Найти отношение времен движения лодок t_А/t_В, если скорость каждой лодки относительно воды в n=1,2 раза больше скорости течения реки.

Ответ: а) t_А/t_В=2,6; б) t_А/t_В=2,4; в) t_А/t_В=2,2; г) t_А/t_В=2;

д) t_А/t_В=1,8.

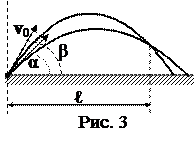
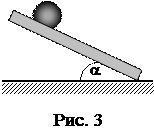
4. Из отверстия шланга, прикрытого пальцем, бьют две струи под углом α=45⁰ и β=60⁰ к горизонту с одинаковой скоростью v=5 м/с. На каком расстоянии по горизонтали струи пересекутся (рис. 3)?

Ответ: а) ℓ=5,24 м; б) ℓ=2,24 м; в) ℓ=3,24 м; г) ℓ=4,24 м;

д) ℓ=1,24 м.

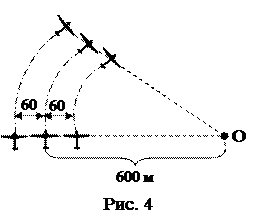5. Три самолета выполняют разворот, двигаясь на расстоянии 60 м друг от друга (рис. 4). Средний самолет летит со скоростью 360 км/ч, двигаясь по дуге окружности радиусом R=600 м. Определить ускорение третьего самолета.

Ответ: а) a₃=14,0 м/с²; б) a₃=15,0 м/с²; в) a₃=16,0 м/с²; г) a₃=17,0 м/с²;

д) a₃=18,0 м/с².

6. Точка соверает гармоническое колебание. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия, равном 0,024 м, скорость точки равна 3 см/с, а при смещении, равном 0,028 м, скорость равна 2 см/с. Найти амплитуду этого колебания.

Ответ: а) А=0,24 м; б) А=0,024 м; в) А=0,34 м; г) А=0,034 м;

д) А=0,014 м.

7. Шар, радиус которого 5 см, подвешен на нити длиной 10 см (рис. 5). Определить погрешность, которую мы делаем, приняв его за математический маятник с длиной 15 см.

Ответ: а) e=22%; б) e=1,2%; в) e=2,2%;

г) e=12%; д) e=0,2%.

8. Однородная палочка подвешена за оба конца на двух одинаковых нитях длиной ℓ=1 м. В состоянии равновесия обе нити параллельны. Найти период Т малых колебаний, возникающих после некоторого поворота палочки вокруг вертикальной оси, проходящей через середину палочки.

Ответ: а) Т=1,20 с; б) Т=1,16 с; в) Т=1,12 с; г) Т=1,08 с;

д) Т=1,04 с.

Вариант № 2

1. Зависимость координаты прямолинейно движущегося тела от времени выражается уравнением x=0,25t⁴-9t⁵. Найти экстремальное значение скорости тела.

Ответ: а) v_max=0,11×10^-6 м/с; б) v_max=1,1 м/с; в) v_max=11×10^-6 м/с;

г) v_max=10,1×10^-6 м/с; д) v_max=2,1×10^-6 м/с.

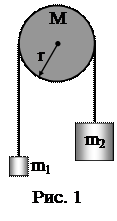2. Две гири массой m₁=1 кг и m₂=2 кг каждая соединены нитью, перекинутой через блок (рис. 1). Радиус блока r=0,1 м и его масса М=1 кг. Найти натяжение нити, к которой подвешена первая гиря. Блок считать однородным диском. Трением пренебречь.

Ответ: а) Т₁=2 Н; б) Т₁=12 Н; в) Т₁=3 Н;

г) Т₁=0,2 Н; д) Т₁=1 Н.

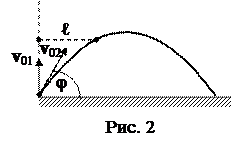3. Два тела бросили одновременно из одной точки: одно – вертикально вверх, другое – под углом j=60⁰ к горизонту (рис. 2). Пренебрегая сопротивлением воздуха, найти расстояние между телами через t=1,70 с.

Ответ: а) l=10 м; б) l=14 м; в) l=18 м; г) l=22 м; д) l=26 м.

4. По внутренней поверхности гладкого вертикального цилиндра радиуса R=0,1 м под углом α=30⁰ к вертикали пускают шарик (рис. 3). Какую начальную скорость ему надо сообщить, чтобы он вернулся в исходную точку, сделав два оборота?

Ответ: а) v=0,77 м/с; б) v=1,77 м/с; в) v=2,77 м/с;

г) v=3,77 м/с; д) v=4,77 м/с.

5. Шарик радиусом 3 см катится равномерно и без скольжения по двум параллельным линейкам, расстояние между которыми равно 4 см (рис. 4), и за 2 с проходит 120 см. С какими ускорением движется верхняя точка шарика?

Ответ: а) а₁=1,0 м/с²; б) а₁=1,2 м/с²;

в) а₁=1,4 м/с²; г) а₁=1,6 м/с²; д) а₁=1,8 м/с².

6. Точка совершает гармоническое колебание. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия, равном 0,024 м, скорость точки равна 3 см/с, а при смещении, равном 0,028 м, скорость равна 2 см/с. Найти период этого колебания.

Ответ: а) Т=1,1 с; б) Т=2,1 с; в) Т=3,1 с;

г) Т=4,1 с; д) Т=5,1 с.

7. Определить период колебания массы m=121 г ртути, находящейся в U - образной трубке (рис. 5). Площадь сечения канала трубки S=0,3 см².

Ответ: а) Т=0,97 с; б) Т=0,77 с; в) Т=0,57 с;

г) Т=0,37 с; д) Т=0,17 с.

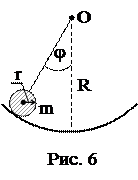8. Сплошной цилиндр радиуса r=0,2 м с моментом инерции I (относительно геометрической оси) и массой m катается без скольжения по внутренней поверхности цилиндра радиуса R=1 м, совершая малые колебания около положения равновесия (рис. 6). Найти период колебаний.

Ответ: а) Т=2,6 с; б) Т=2,4 с; в) Т=2,2 с;

г) Т=2,0 с; д) Т=1,6 с.

Вариант № 3

1. Одновременно из одного пункт выезжают две автомашины, которые движутся в одном направлении неравномерно. Зависимость пройденного автомобилями пути от времени выражается уравнениями S₁=t-0,2t² и S₂=2t+t²-0,6t³. Найти относительную скорость автомашин в момент времени t=5 с.

Ответ: а) v₁₂=2 м/с; б) v₁₂=1,2 м/с; в) v₁₂=22 м/с; г) v₁₂=32 м/с;

д) v₁₂=42 м/с.

2. Две гири массами m₁=1 кг и m₂=2 кг соединены нитью, перекинутой через блок (рис. 1). Радиус блока r=0,1 м и его масса M=1 кг. Найти натяжение нити, к которой подвешена вторая гиря. Блок считать однородным диском. Трением пренебречь.

Ответ: а) Т₂=1,4 Н; б) Т₂=0,4 Н; в) Т₂=14 Н;

г) Т₂=4 Н; д) Т₂=24 Н.

3. Две частицы движутся с ускорением g в однородном поле тяжести. В начальный момент частицы находились в одной точке и имели скорости v₀₁=3,0 м/с и v₀₂=4,0 м/с, направленные горизонтально и в противоположные стороны. Найти расстояние между частицами в момент, когда векторы их скоростей окажутся взаимно перпендикулярными (α=90⁰) (рис. 2).

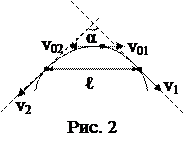Ответ: а) l=1,5 м; б) l=2 м; в) l=2,5 м; г) l=3 м; д) l=3,5 м.

4. В момент времени, когда модуль скорости v=10⁶ м/с, ускорение частицы а=10⁴ м/с² и направлено под углом 30⁰ к вектору скорости. На сколько увеличится модуль скорости за время Δt=10^-2 с?

Ответ: а) Δv=0,87∙10² м/с; б) Δv=0,77∙10² м/с;

в) Δv=0,67∙10² м/с; г) Δv=0,57∙10² м/с; д) Δv=0,47∙10² м/с.

5. Шарик радиусом 3 см катится равномерно и без скольжения по двум параллельным линейкам, расстояние между которыми равно 4 см (рис. 3), и за 2 с проходит 120 см. С какими ускорением движется нижняя точка шарика?

Ответ: а) а= -0,5 м/с²; б) а= -0,4 м/с²;

в) а= -0,3 м/с²; г) а= -0,2 м/с²; д) а= -0,1 м/с².

6. Точка одновременно совершает два гармонических колебания, происходящих по одной и той же прямой. Амплитуды колебаний одинаковы, периоды равны 0,1 с и 0,102 с. Найти период изменения амплитуды результирующего колебания (период биений).

Ответ: а) Т_б=1,1 с; б) Т_б=2,1 с; в) Т_б=3,1 с; г) Т_б=4,1 с; д) Т_б=5,1 с.

7. Предположим, что по одному из диаметров Земли просверлен канал. Принимая Землю за однородный шар, найти время t движения тела от поверхности Земли до ее центра. Плотность Земли принять равной r=5,5×10³ кг/м³

Ответ: а) t=23 мин; б) t=21 мин; в) t=19 мин; г) t=17 мин;

д) t=15 мин.

8. Сплошной шар радиуса r=0,2 м с моментом инерции I (относительно геометрической оси) и массой m катается без скольжения по внутренней поверхности цилиндра радиуса R=1 м, совершая малые колебания около положения равновесия (рис. 4). Найти период колебаний.

Ответ: а) Т=2,42 с; б) Т=2,32 с; в) Т=2,22 с;

г) Т=2,12 с; д) Т=2,02 с.

Вариант № 4

1. Винт аэросаней вращается с частотой n =6 с^-1. Скорость поступательного движения саней v=54 км/ч. С какой скоростью движется один из концов винта, если радиус винта R=1 м?

Ответ: а) v=20,6 м/с; б) v=30,6 м/с; в) v=40,6 м/с; г) v=50,6 м/с; д) v=60,6 м/с.

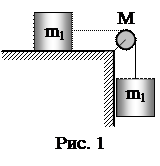2. Блок массой M=1 кг укреплен на конце стола. Гири равной массы m₁=m₂=1 кг соединены нитью, перекинутой через блок. Коэффициент трения одной из гирь о стол равен 0,1 (рис. 1). Найти ускорение, с которым движутся гири.

Ответ: а) а=1,53 м/с²; б) а=2,53 м/с²;

в) а=3,53 м/с²; г) а=2 м/с²; д) а=0,53 м/с².

3. Кабина лифта, у которой расстояние от пола до потолка равно 2,7 м, начала подниматься с постоянным ускорением 1,2 м/с². Через 2,0 с после начала подъема с потолка кабины стал падать болт. Найти время свободного падения болта.

Ответ: а) t=0,5 с; б) t=0,7 с; в) t=0,9 с; г) t=1,1 с; д) t=1,3 с.

4. В момент времени, когда модуль скорости v=10⁶ м/с, ускорение частицы а=10⁴ м/с² и направлено под углом 30⁰ к вектору скорости. На какой угол изменится направление скорости за время Δt=10^-2 с?

Ответ: а) Δφ=1∙10^-5 рад; б) Δφ=2∙10^-5 рад;

в) Δφ=3∙10^-5 рад; г) Δφ=4∙10^-5 рад; д) Δφ=5∙10^-5 рад.

5. На рисунке 2 изображен прибор для пояснения зависимости центробежной силы от массы и расстояния от оси вращения. Шары А и В имеют диаметры 3 см и 2 см. Соединяющий шары шнур имеет длину l=10,5 см. На каком расстоянии x от оси ОО должен быть помещен центр шара А, чтобы при вращающемся приборе шары удерживались на неизменном расстоянии от оси? Шары сделаны из одного и того же материала. Объемом канала, просверленного внутри шаров, можно пренебречь.

Ответ: а) x=1,6 см; б) x=1,8 см; в) x=2,0 см; г) x=2,2 см;

д) x=2,4 см.

6. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями 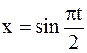, y=cospt. Найти уравнение траектории точки.

Ответ: а) y=1-x²; б) y=1+3x²; в) y=1-3x²; г) y=1+2x²; д) y=1-2x².

7. Каков логарифмический декремент затухания маятника длиной 0,8 м, если его начальная амплитуда 5⁰, а через время 5 мин амплитуда равна 0,5⁰?

Ответ: а) l=0,014; б) l=0,024; в) l=0,14; г) l=0,24; д) l=0,034.

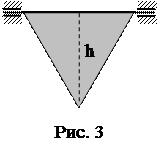8. Достаточно тонкая пластинка из однородного материала имеет форму равностороннего треугольника высоты h=0,2 м (рис. 3). Она может вращаться вокруг горизонтальной оси, совпадающей с одной из сторон пластинки. Найти период малых колебаний такого физического маятника.

Ответ: а) Т=1,03 с; б) Т=0,93 с; в) Т=0,83 с;

г) Т=0,73 с; д) Т=0,63 с.

Вариант № 5

1. На столе лежит доска массой М=1 кг, а на доске – груз массой m=2 кг. Какую силу нужно приложить к доске, чтобы доска выскользнула из – под груза? Коэффициент трения между грузом и доской m₁=0,25, а между доской и столом m₂=0,5.

Ответ: а) F≥2,21 Н; б) F≥22,1 Н; в) F≥12,1 Н; г) F≥32,1 Н; д) F≥15,1 Н.

2. Блок массой M=1 кг укреплен на конце стола. Гири равной массы m₁=m₂=1 кг соединены нитью, перекинутой через блок (рис. 1). Коэффициент трения гири, лежащей на столе, о стол равен 0,1. Найти натяжение нити, к которой прикреплена гиря, лежащая на столе.

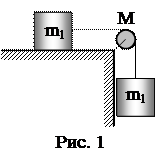Ответ: а) Т₁=0,5 Н; б) Т₁=1,5 Н; в) Т₁=2,5 Н; г) Т₁=4,5 Н; д) Т₁=3,5 Н.

3. Кабина лифта, у которой расстояние от пола до потолка равно 2,7 м, начала подниматься с постоянным ускорением 1,2 м/с². Через 2,0 с после начала подъема с потолка кабины стал падать болт. Найти перемещение и путь болта за время свободного падения в системе отсчета, связанной с шахтой лифта.

Ответ: а) Dr=0,7 м; S=1,3 м; б) Dr=0,5 м; S=1,2 м; в) Dr=0,6 м; S=1,1 м; г) Dr=0,8 м; S=1 м; д) Dr=0,4 м; S=1,4 м.

4. В момент времени, когда модуль скорости v=10⁶ м/с, ускорение частицы а=10⁴ м/с² и направлено под углом 30⁰ к вектору скорости. Какова угловая скорость вращения вектора скорости в момент времени t=10^-2 c?

Ответ: а) ω=6∙10^-3 рад/с; б) ω=5∙10^-3 рад/с; в) ω=4∙10^-3 рад/с;

г) ω=3∙10^-3 рад/с; д) ω=2∙10^-3 рад/с.

5. Грузик привязан к нити, другой конец которой прикреплен к потолку. Вследствие толчка грузик движется по окружности, плоскость которой отстоит от потолка на h=1,5 м. Какова частота оборотов грузика?

Ответ: а) n=0,1 с^-1; б) n=0,8 с^-1; в) n=0,2 с^-1; г) n=0,6 с^-1;

д) n=0,4 с^-1.

6. Точка одновременно совершает два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражается уравнениями x=0,5sinwt, y=coswt. Найти уравнение траектории точки.

Ответ: а) y²+16x²=4; б) y²-16x²=4; в) y²+12x²=4; г) y²-12x²=4;

д) y²+10x²=4.

7. Какова общая сумма путей, пройденных взад и вперед колеблющейся точкой до полного затухания колебаний, если амплитуда первого колебания равна 1 мм, а логарифмический декремент затухания равен 0,002?

Ответ: а) S=2 м; б) S=3 м; в) S=5 м; г) S=6 м; д) S=7 м.

8. Сплошной однородный диск с радиусом r=0,1 м колеблется около оси, перпендикулярной к плоскости диска и проходящей через край диска (рис. 2). Какой длины ℓ должен быть математический маятник, имеющий тот же период колебаний, что и диск?

Ответ: а) ℓ=0,15 м; б) ℓ=0,25 м; в) ℓ=0,35 м;

г) ℓ=0,015 м; д) ℓ=0,025 м.

Вариант № 6

1. На вал радиусом 1 см намотана нить, к концу которой привязана гиря. Опускаясь равноускоренно, гиря прошла расстояние 200 см за 10 с. Найти полное ускорение точки, лежащей на поверхности вала, в конечный момент движения.

Ответ: а) a=1,6 м/с²; б) a=2,6 м/с²; в) a=3,6 м/с²; г) a=4,6 м/с²;

д) a=5,6 м/с².

2. Блок массой M=1 кг укреплен на конце стола. Гири равной массы m₁=m₂=1 кг соединены нитью, перекинутой через блок (рис. 1). Коэффициент трения одной из гирь о стол равен 0,1. Найти натяжение нити, к которой прикреплена вторая гиря.

Ответ: а) Т₂=1,3 Н; б) Т₂=2,3 Н; в) Т₂=3,3 Н; г) Т₂=6,3 Н; д) Т₂=8,3 Н.

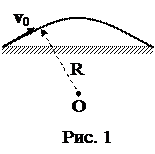
3. Из пушки (рис. 2) выпустили последовательно два снаряда со скоростью v₀=300 м/с: первый – под углом a₁=45⁰ к горизонту, второй – под углом a₂=30⁰ к горизонту. Пренебрегая сопротивлением воздуха, найти интервал времени между выстрелами, при котором снаряды столкнутся друг с другом.

Ответ: а) Dt=10 с; б) Dt=12 с; в) Dt=14 с; г) Dt=16 с; д) Dt=18 с.

4. Тело движется по окружности радиуса r=2 м со скоростью, которая линейно увеличивается во времени: 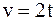. Определить модуль полного ускорения тела в момент времени t=2 с.

Ответ: а) а=6,25 м/с²; б) а=7,25 м/с²; в) а=8,25 м/с²;

г) а=5,25 м/с²; д) а=4,25 м/с².

5. Две прочные линейки расположены параллельно друг другу на расстоянии d=2см под углом a=5⁰ к горизонту (рис. 3). С каким ускорением будет катиться по ним шарик, радиус которого r=1,5 см? Скольжение отсутствует.

Ответ: а) а=0,2 м/с²; б) а=0,3 м/с²;

в) а=0,1 м/с²; г) а=0,5 м/с²; д) а=0,1 м/с².

6. Складываются два колебания одинакового направления и одинакового периода x₁=sinpt и x₂=sinp(t+0,5). (Длина – в сантиметрах, время – в секундах.) Определить амплитуду А результирующего колебания.

Ответ: а) А=1,2 см; б) А=1,4 см; в) А=1,6 см; г) А=1,8 см;

д) А=2,0 см.

7. Амплитуды скорости вынужденных колебаний при частотах вынуждающей силы n₁=200 Гц и n₂=300 Гц равны между собой. Принимая, что амплитуда вынуждающей силы в обоих случаях одна и та же, найти частоту, соответствующую резонансу скорости.

Ответ: а) n=245 Гц; б) n=345 Гц; в) n=145 Гц; г) n=445 Гц;

д) n=45 Гц.

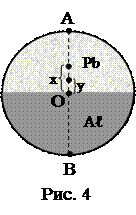8. Диск радиуса R=0,2 м состоит из двух половин одинаковой толщины: одна половина алюминиевая (плотность r=2,5×10³ кг/м³), вторая – свинцовая (плотность r=10×10³ кг/м³). Расстояние центра масс всего диска от центра диска y=0,05 м. Расстояние центра масс полудиска от центра диска x=0,083 м (рис. 4). Определить период малых колебаний диска относительно точки А. Ось перпендикулярна плоскости диска.

Ответ: а) Т_А=0,18 с; б) Т_А=0,13 с; в) Т_А=0,23 с;

г) Т_А=0,33 с; д) Т_А=0,28 с.

Вариант № 7

1. Мяч, брошенный горизонтально, ударяется о стенку, находящуюся на расстоянии 5 м от места бросания. Высота места удара мяча о стенку на 1 м меньше высоты, с которой брошен мяч. Под каким углом мяч подлетает к поверхности стенки? Сопротивление воздуха не учитывать.

Ответ: а) a=21⁰; б) a=31⁰; в) a=11⁰; г) a=15⁰; д) a=41⁰.

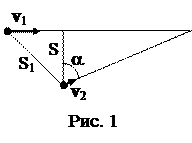2. Человек находится на расстоянии S=50 м от прямой дороги (рис. 1), по которой приближается автомобиль со скоростью v₁=10 м/с. По какому направлению должен бежать человек, чтобы встретиться с автомобилем, если автомобиль находится на расстоянии S₁=200 м от человека и если человек может бежать со скоростью v₂=3 м/с?

Ответ: а) a=16,4⁰; б) a=26,4⁰; в) a=36,4⁰; г) a=46,4⁰; д) a=56,4⁰.

3. Небольшое тело заставили двигаться снизу вверх по наклонной плоскости, составляющей угол a=15⁰ с горизонтом. Найти коэффициент трения, если время подъема тела оказалось в n=2,0 раза меньше времени спуска (рис. 2).

Ответ: а) m=0,14; б) m=0,16; в) m=0,18;

г) m=0,20; д) m=0,22.

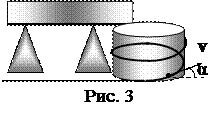4. Для экономии места въезд на один из высочайших в Японии мостов устроен в виде винтовой линии, обвивающей цилиндр радиуса R=40 м (рис. 3). Полотно дороги составляет угол α=20⁰ с горизонтальной плоскостью. Каково ускорение автомобиля, движущегося с постоянной по модулю скоростью v=72 км/ч?

Ответ: а) а=5,8 м/с²; б) а=6,8 м/с²; в) а=7,8 м/с²; г) а=8,8 м/с²;

д) а=9,8 м/с².

5. Вертикальный столб высотой h=5 м подпиливается у основания и падает на Землю (рис. 4). Определить линейную скорость его верхнего конца в момент удара о Землю.

Ответ: а) v=8 м/с; б) v=10 м/с; в) v=12 м/с;

г) v=14 м/с; д) v=7 м/с.

6. Складываются два колебания одинакового направления и одинакового периода x₁=sinpt и x₂=sinp(t+0,5). (Длина – в сантиметрах, время – в секундах.) Определить начальную фазу j_о результирующего колебания.

Ответ: а) j₀=p/2; б) j₀=p/3; в) j₀=p/4; г) j₀=p; д) j₀=p/6.

7. Амплитуды смещений вынужденных колебаний при частотах вынуждающей силы n₁=200 Гц и n₂=300 Гц, равны между собой. Найти частоту, соответствующую резонансу смещений.

Ответ: а) n=355 Гц; б) n=255 Гц; в) n=155 Гц; г) n=55 Гц;

д) n=555 Гц.

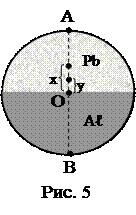8. Диск радиуса R=0,2 м состоит из двух половин одинаковой толщины: одна половина алюминиевая (плотность r=2,5×10³ кг/м³), вторая – свинцовая (плотность r=10×10³ кг/м³) (рис. 5). Расстояние центра масс всего диска от центра диска y=0,05 м. Расстояние центра масс полудиска от центра диска x=0,083 м. Определить период малых колебаний диска относительно точки В. Ось перпендикулярна плоскости диска.

Ответ: а) Т_В=0,53 с; б) Т_В=0,43 с; в) Т_В=0,33 с; г) Т_В=0,23 с; д) Т_В=0,13 с.

Вариант № 8

1. Тело брошено со скоростью 20 м/с вверх под углом 30^о к горизонту (рис. 1). Найти радиус кривизны траектории в точке, в которой окажется тело через одну секунду после начала движения.

Ответ: а) R=31 м; б) R=21 м; в) R=11 м;

г) R=1,1 м; д) R=3,1 м.

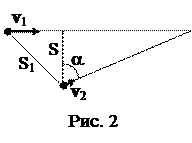2. Человек находится на расстоянии S=50 м от прямой дороги, по которой приближается автомобиль со скоростью v₁=10м/с (рис. 2). Определить наименьшую скорость, с которой должен бежать человек, чтобы встретиться с автомобилем, если автомобиль находится на расстоянии S₁=200 м от человека.

Ответ: а) v₂=0,5 м/с; б) v₂=1,5 м/с; в) v₂=3,5 м/с; г) v₂=4,5 м/с;

д) v₂=2,5 м/с.

3. Небольшое тело А начинает скользить с вершины клина, основание которого а=2,10 м. Коэффициент трения между телом и поверхностью клина m=0,14 (рис. 3). При каком значении угла a время соскальзывания будет наименьшим?

Ответ: а) a=69⁰; б) a=59⁰; в) a=49⁰; г) a=39⁰; д) a=29⁰.

4. Материальная точка начинает двигаться по окружности радиусом r=12,5 см с постоянным тангенциальным ускорением a_τ=0,5 м/с². Определить момент времени, при котором вектор ускорения 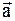образует с вектором скорости 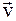угол α=45⁰.

Ответ: а) t=1 с; б) t=2 с; в) t=3 с; г) t=4 с; д) t=5 с.

5. Вертикальный столб высотой h=5 м подпиливается у основания и падает на Землю. Какая точка столба будет в любой момент падения столба иметь ту же скорость, какую имело бы тело, падая с той же высоты, как и данная точка (рис. 4)?

Ответ: а) h₁=4/3 h; б) h₁=1/3 h; в) ; г) h₁=2/3 h; д) h₁=5/3 h.

6. Складываются два колебания одинакового направления и одинакового периода x₁=sinpt и x₂=sinp(t+0,5). (Длина – в сантиметрах, время – в секундах.) Получить уравнение результирующего колебания.

Ответ: а) x=1,4sinπ(t-1/2); б) x=1,4sinπ(t+1/2);

в) x=1,4sinπ(t-1/4); г) x=1,4sinπ(t+1/4); д) x=1,4sinπ(t+1/3).

7. Амплитуда смещения вынужденных колебаний при очень малой частоте равна x₀=2 мм, а при резонансе равна X₀=16 мм. Предполагая, что декремент затухания меньше единицы, определить его.

Ответ: а) D=0,25; б) D=0,3; в) D=0,4; г) D=0,2; д) D=0,1.

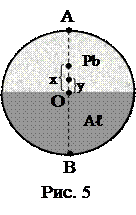8. Диск радиуса R=0,2 м состоит из двух половин одинаковой толщины: одна половина алюминиевая (плотность r=2,5×10³ кг/м³), вторая – свинцовая (плотность r=10×10³ кг/м³) (рис. 5). Расстояние центра масс всего диска от центра диска y=0,05 м. Расстояние центра масс полудиска от центра диска x=0,083 м. Каково будет отношение периодов колебаний этого диска вокруг оси перпендикулярной к плоскости диска, проходящей через точку А и В?

Ответ: а) Т_А/Т_В=0,69; б) Т_А/Т_В=0,59;

в) Т_А/Т_В=0,49; г) Т_А/Т_В=0,39; д) Т_А/Т_В=0,29.

Вариант № 9

1. Камень, брошенный со скоростью 12 м/с под углом 45^о к горизонту (рис. 1), упал на землю на расстоянии L от места бросания. С какой высоты надо бросить камень в горизонтальном направлении, чтобы при той же начальной скорости он упал на то же место?

Ответ: а) h=6,35 м; б) h=7,35 м; в) h=8,35 м; г) h=9,35 м; д) h=10,35 м.

2. Наблюдатель, стоявший в момент начала движения электропоезда у его переднего края, заметил, что первый вагон прошел мимо него за время t=4 с. Сколько времени будет двигаться мимо наблюдателя 7 – й вагон? Движение считать равномерно ускоренным.

Ответ: а) t₇=0,5 с; б) t₇=0,6 с; в) t₇=0,7 с; г) t₇=0,8 с; д) t₇=0,9 с.

3. Небольшое тело А (рис. 2) начинает скользить с вершины клина, основание которого а=2,10 м. Коэффициент трения между телом и поверхностью клина m=0,14. Чему равно наименьшее время соскальзывания при угле a=49⁰?

Ответ: а) t_min=1,6 с; б) t_min=1,4 с; в) t_min=1,2 с; г) t_min=1,0 с;

д) t_min=0,8 с.

4. Материальная точка начинает двигаться по окружности радиусом r=12,5 см с постоянным тангенциальным ускорением равным a_τ=0,5 м/с². Определить путь, пройденный движущейся точкой за промежуток времени, по прошествии которого вектор ускорения 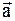образует с вектором скорости 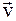угол α=45⁰.

Ответ: а) S=6,25 см; б) S=5,25 см; в) S=7,25 см; г) S=4,25 см;

д) S=8,25 см.

5. Массивное колесо, насаженное на оси, поддерживается двумя закрепленными нитями (рис. 3). Ось вращения колеса горизонтальна. Нити постепенно раскручиваются с оси, а колесо опускается. Определить натяжение F каждой из двух нитей, если масса колеса вместе с осью m=1 кг, момент инерции относительно этой оси I=2,5×10^{-3 кг}×м² и радиус оси r=5 мм.

Ответ: а) F=5,85 Н; б) F=4,85 Н; в) F=3,85 Н;

г) F=2,85 Н; д) F=1,85 Н.

6. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых следующими уравнениями x=sin 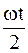; y=coswt. Найти уравнение траектории точки.

Ответ: а) y=1-x²; б) y=1+3x²; в) y=1-3x²; г) y=1+2x²; д) y=1-2x².

7. Точка совершает гармонические колебания вдоль некоторой прямой с периодом T=0,60 с и амплитудой x₀=10,0 см. Найти среднюю скорость точки за время, в течение которого она проходит путь, равный x₀/2: а) из крайнего положения; б) из положения равновесия.

Ответ: а) <v₁>=1,5 м/с; <v₂>=1,5 м/с; б) <v₁>=2,5 м/с;

<v₂>=2,0 м/с; в) <v₁>=0,3 м/с; <v₂>=1,5 м/с; г) <v₁>=0,5 м/с;

<v₂>=1,0 м/с; д) <v₁>=2,0 м/с; <v₂>=1,5 м/с.

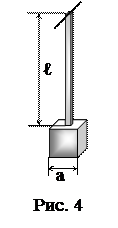8. Физический маятник состоит из стержня квадратного сечения, подвешенного за конец, и груза, прикрепленного на другом конце (рис. 4). Груз имеет форму куба с ребром а=40 см, а стержень – длину ℓ=400 мм и сторону сечения b=4 мм; груз и стержень сделаны из одного материала. Найти приближенное значение периода колебаний Т такого маятника (при расчете можно полагать стержень достаточно тонким).

Ответ: а) Т»1,89 с; б) Т»1,79 с; в) Т»1,59 с;

г) Т»2,29 с; д) Т»1,29 с.

Вариант № 10

1. Наклонная плоскость составляет угол 37° с линией горизонта. На наклонной плоскости лежит брусок массой m₁=1 кг. Шнур, привязанный одним концом к бруску, перекинут через неподвижный блок, укрепленный в верхнем конце наклонной плоскости. К другому концу шнура, свисающему с блока, подвешена гирька массой m₂=0,4 кг (рис. 1). Коэффициент трения равен 0,2. С каким ускорением будет двигаться брусок? В начальный момент скорость равна нулю.

Ответ: а) a=0,19 м/с²; б) a=0,9 м/с²; в) a=0,29 м/с²; г) a=0,39 м/с²; д) a=0,49 м/с².

2. Наблюдатель, стоящий на платформе, заметил, что первый вагон электропоезда, приближающегося к станции, прошел мимо него в течение t₁=4 с, а второй – в течение t₂=5 с. После этого передний край поезда остановился на расстоянии S=75 м от наблюдателя. Считая движение поезда равномерно замедленным, определить его ускорение.

Ответ: а) a=-0,45 м/с²; б) a=-0,35 м/с²;

в) a=-0,25 м/с²; г) a=-0,15 м/с²; д) a=-0,05 м/с².

3. В установке (рис. 2) шарик 1 имеет массу в n=1,8 раза больше массы стержня 2. Длина последнего l=100 см. Шарик установили на одном уровне с нижним концом стержня и отпустили. Через сколько времени он поравняется с верхним концом стержня? Массой блоков и нитей, а также трением пренебречь.

Ответ: а) t=1,6 с; б) t=1,5 с; в) t=1,0 с; г) t=1,2 с; д) t=1,4 с.

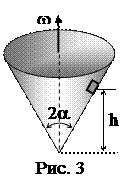4. На внутренней поверхности конической воронки с углом 2a (a=30⁰) при вершине на высоте h=0,1 м от вершины находится малое тело. Коэффициент трения между телом и поверхностью воронки равен k=0,1. Найти минимальную угловую скорость вращения конуса вокруг вертикальной оси, при которой тело будет неподвижно в воронке (рис. 3).

Ответ: а) w=15,4 рад/с; б) w=13,4 рад/с;

в) w=11,4 рад/с; г) w=16,4 рад/с; д) w=17,4 рад/с.

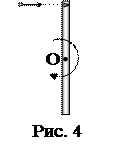5. Деревянный стержень с массой m=1 кг и длиной l=0,4 м может вращаться около оси, проходящей через его середину перпендикулярно к стержню (рис. 4). В конец стержня попадает пуля с массой m₁=10 г, летящая перпендикулярно к оси и к стержню со скоростью v=200 м/с. Определить угловую скорость, которую получит стержень, если пуля застрянет в нем.

Ответ: а) w=29 рад/с; б) w=27 рад/с;

в) w=25 рад/с; г) w=23 рад/с; д) w=21 рад/с.

6. Материальная точка совершает затухающие колебания с периодом 2 с. За 10 с амплитуда уменьшилась в три раза. Найти логарифмический декремент затухания.

Ответ: а) l=0,22; б) l=0,32; в) l=0,12; г) l=0,42; д) l=0,42.

7. В момент времени t=0 частица начинает двигаться вдоль оси x так, что ее скорость меняется по закону v=35cospt см/с, где t – в секундах. Найти путь, который пройдет эта частица за первые t=2,80 с после начала движения.

Ответ: а) S=0,2 м; б) S=0,3 м; в) S=0,4 м; г) S=0,5 м; д) S=0,6 м.

8. На горизонтальной плоскости находится цилиндр массой m=2 кг. К оси цилиндра прикреплены две одинаковые горизонтально расположенные спиральные пружины, другие концы которых закреплены в стене. Коэффициент упругости пружин равен k=200 Н/м; пружины могут работать как на растяжение, так и на сжатие (рис. 5). Найти период малых колебаний цилиндра, которые возникнут, если вывести его из положения равновесия и дать возможность кататься без скольжения по горизонтальной плоскости.

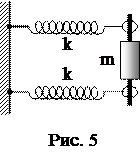Ответ: а) Т=0,84 с; б) Т=0,74 с; в) Т=0,64 с;

г) Т=0,54 с; д) Т=0,44 с.

Вариант № 11

1. Наклонная плоскость составляет угол 37° с линией горизонта. На наклонной плоскости лежит брусок массой 1 кг. Шнур, привязанный одним концом к бруску, перекинут через неподвижный блок, укрепленный в верхнем конце наклонной плоскости. К другому концу шнура, свисающему с блока, подвешена гирька массой 0,4 кг (рис. 1). Коэффициент трения равен 0,2. Чему равно натяжение нити? В начальный момент скорость равна нулю.

Ответ: а) Т=3,1 Н; б) Т=3,3 Н; в) Т=3,5 Н; г) Т=3,7 Н; д) Т=3,8 Н.

2. С какой скоростью должен лететь самолет, чтобы за время t=1 ч пролететь точно по направлению на север путь S=200 км, если во время полета дует северо-восточный ветер под углом 35⁰ к меридиану со скоростью 30 км/ч?

Ответ: а) v=325 км/ч; б) v=225 км/ч; в) v=425 км/ч;

г) v=525 км/ч; д) v=625 км/ч.

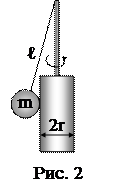3. Материальная точка движется по окружности радиуса R=20 м согласно уравнению S=8t+0,2t³. Найти полное ускорение материальной точки в момент времени t=3 с.

Ответ: а) a=8,5 м/с²; б) a=8,8 м/с²; в) a=9,1 м/с²; г) a=9,4 м/с²; д) a=9,7 м/с².

4. Шарик радиусом R=0,1 м висит на нити длиной ℓ=1 м и касается вертикального цилиндра радиусом r=0,2 м, установленного на оси центробежной машины (рис. 2). При какой угловой скорости w вращения центробежной машины шарик перестанет давить на стенку цилиндра?

Ответ: а) w=1,93 рад/с; б) w=2,93 рад/с; в) w=3,93 рад/с;

г) w=4,93 рад/с; д) w=5,93 рад/с.

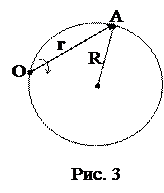5. Частица А движется по окружности радиусом R=50 см так, что ее радиус – вектор r относительно точки О (рис. 3) поворачивается с постоянной угловой скоростью w=0,40 рад/с. Найти модуль скорости частицы.

Ответ: а) v=0,1 м/с; б) v=0,2 м/с;

в) v=0,5 м/с; г) v=0,3 м/с; д) v=0,4 м/с.

6. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия, равном 0,024 м, скорость точки равна 3 см/с, а при смещении, равном 0,028 м, скорость равна 2 см/с. Найти амплитуду этого колебания.

Ответ: а) А=0,24 м; б) А=0,024 м; в) А=0,34 м; г) А=0,034 м;

д) А=0,014 м.

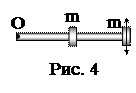7. На стержне длиной 30 см укреплены два одинаковых грузика: один – в середине стержня, другой – на одном из его концов (рис. 4). Стержень с грузиками колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить период колебаний такого маятника. Массой стержня пренебречь.

Ответ: а) Т=1,62 с; б) Т=1,42 с; в) Т=1,82 с; г) Т=1,52 с;

д) Т=1,72 с.

8. Частицу сместили из положения равновесия на расстояние а=1,0 см и предоставили самой себе. Какой путь пройдет, колеблясь, эта частица до полной остановки, если логарифмический декремент затухания l=0,020?

Ответ: а) S=6,0 м; б) S=5,0 м; в) S=4,0 м; г) S=3,0 м; д) S=2,0 м.

Вариант № 12

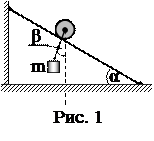
1. По тросу, натянутому под углом 30^о к линии горизонта, скатывается блок (рис. 1), к обойме которого на шнуре подвешен груз массой 2 кг. Определить натяжение шнура. Ускорение движения блока и груза равно 3,5 м/с². Прогибом троса и массой блока пренебречь.

Ответ: а) Т=7 Н; б) Т=27 Н; в) Т=0,7 Н;

г) Т=17 Н; д) Т=1,7 Н.

2. Камень брошен вертикально вверх со скоростью v₀=15 м/с. Через сколько времени он будет на высоте h=10 м?

Ответ: а) t₁=0,98 с; t₂=2,1 с; б) t₁=0,88 с; t₂=0,1 с; в) t₁=0,78 с; t₂=0,21 с; г) t₁=0,68 с; t₂=1,1 с; д) t₁=0,58 с; t₂=0,91 с.

3. Закон движения точки по кривой выражается уравнением S=4t²+t³. Найти путь, пройденный точкой за промежуток времени от t₁=1 с до t₂=4c.

Ответ: а) S=123 м; б) S=120 м; в) S=126 м; г) S=129 м;

д) S=117 м.

4. В вагоне поезда, идущего по закруглению железнодорожного пути, сделанному, как обычно, с уклоном внутрь, на пружинных весах подвешено тело. Весы показывают увеличение веса тела на 10% по сравнению с весом того же тела, измеренным в поезде, идущем прямолинейно с постоянной скоростью. Весы могут свободно поворачиваться около точки подвеса и на закруглении остаются висеть перпендикулярно к полу вагона. Найти радиус кривизны пути R, если поезд идет со скоростью v=10 м/с.

Ответ: а) R=237 м; б) R=227 м; в) R=217 м; г) R=247 м;

д) R=207 м.

5. Частица А движется по окружности радиусом R=50 см так, что ее радиус – вектор r относительно точки О –поворачивается с постоянной угловой скоростью w=0,40 рад/с. Найти модуль вектора ее полного ускорения (рис. 2).

Ответ: а) а=0,12 м/с²; б) а=0,52 м/с²;

в) а=0,22 м/с²; г) а=0,32 м/с²; д) а=0,032 м/с².

6. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия, равном 0,024 м, скорость точки равна 3 см/с, а при смещении, равном 0,028 м, скорость равна 2 см/с. Найти период этого колебания.

Ответ: а) Т=1,1 с; б) Т=2,1 с; в) Т=3,1 с; г) Т=4,1 с; д) Т=5,1 с.

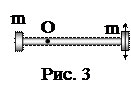7. На концах тонкого стержня длиной 3 см укреплены одинаковые грузы, по одному на каждом конце. Стержень с грузиками колеблется около горизонтальной оси, проходящей через точку, удаленную на 1 см от одного из концов стержня. Определить период колебания такого физического маятника (рис. 3).

Ответ: а) Т=1,62 с; б) Т=1,42 с; в) Т=1,82 с;

г) Т=1,52 с; д) Т=1,72 с.

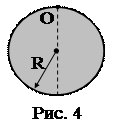8. Однородный диск радиусом R=13 см может вращаться вокруг горизонтальной оси, перпендикулярной к его плоскости и проходящей через край диска (рис. 4). Найти период малых колебаний этого диска в поле тяжести Земли, если логарифмический декремент затухания l=1,00.

Ответ: а) T=0,6 с; б) T=0,7 с; в) T=0,8 с; г) T=0,9 с; д) T=1,0 с.

Вариант № 13

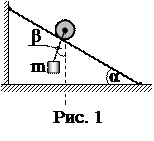1. По тросу, натянутому под углом 30^о к линии горизонта, скатывается блок, к обойме которого на шнуре подвешен груз массой 2 кг (рис. 1). Определить угол, который составляет шнур с вертикальной линией. Ускорение движения блока и груза равно 3,5 м/с². Прогибом троса и массой блока пренебречь.

Ответ: а) b=15⁰; б) b=17⁰; в) b=19⁰; г) b=18⁰; д) b=21⁰.

2. Камень брошен вертикально вверх со скоростью 15 м/с. Через сколько времени он будет на высоте h=12 м?

Ответ: а) t₁=0,98 с; t₂=2,1 с; б) t₁=0,88 с; t₂=0,1 с; в) t₁=0,78 с; t₂=0,21 с; г) t₁=0,68 с; t₂=1,1 с; д) Не будет.

3. Закон движения точки по кривой выражается уравнением S=4t²+t³. Найти радиус кривизны траектории в том месте, где будет находиться эта точка в момент времени t=4 с, если нормальное ускорение в этот момент равно 8 м/с².

Ответ: а) R=800 м; б) R=780 м; в) R=820 м; г) R=760 м;

д) R=840 м.

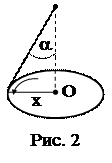
4. Металлическое кольцо, подвешенное на нити к оси центробежной машины (рис. 2), равномерно вращается с угловой скоростью w=5 рад/с. Нить составляет угол a=30⁰ с осью. Найти расстояние от центра кольца до оси вращения.

Ответ: а) x=0,13 м; б) x=0,33 м; в) x=0,23 м;

г) x=0,43 м; д) x=0,53 м.

5. Колесо вращается вокруг неподвижной оси так, что угол j его поворота зависит от времени по закону j=at², где а=0,20 рад/с². Найти полное ускорение точки А на ободе колеса в момент времени t=2,5 с, если линейная скорость точки А в этот момент v=0,65 м/с.

Ответ: а) а=0,55 м/с²; б) а=0,65 м/с²; в) а=0,75 м/с²;

г) а=0,85 м/с²; д) а=0,95 м/с².

6. Точка одновременно совершает два гармонических колебания, происходящих по одной и той же прямой. Амплитуды колебаний одинаковы, периоды равны 0,1 с и 0,102 с. Найти период изменения амплитуды результирующего колебания (период биений).

Ответ: а) Т_б=1,1 с; б) Т_б=2,1 с; в) Т_б=3,1 с; г) Т_б=4,1 с;

д) Т_б=5,1 с.

7. На концах тонкого стержня длиной 3 см укреплены одинаковые грузы по одному на каждом конце (рис. 3). Стержень с грузиками колеблется около горизонтальной оси, проходящей через точку, удаленную на 1 см от одного из концов стержня. Определить частоту колебаний такого физического маятника.

Ответ: а) n=0,1 Гц; б) n=0,3 Гц; в) n=0,5 Гц; г) n=0,7 Гц;

д) n=0,9 Гц.

8. На горизонтальной плоскости с коэффициентом трения m=0,10 лежит брусок массой m=0,50 кг, соединенный горизонтальной недеформированной пружиной со стенкой. Жесткость пружины k=2,45 Н/см, а ее масса пренебрежимо мала. Брусок сместили так, что пружинка растянулась на x₀=3,0 см, а затем отпустили (рис. 4). Найти период колебаний бруска.

Ответ: а) T=0,48 с; б) T=0,38 с; в) T=0,28 с; г) T=0,18 с;

д) T=0,58 с.

Вариант № 14

1. Струя воды ударяется о неподвижную плоскость, поставленную под углом=60^o к направлению движения струи. Скорость v струи равна 20 м/с, площадь S ее поперечного сечения равна 5 см². Определить силу F давления струи на плоскость.

Ответ: а) F=46 Н; б) F=146 Н; в) F=246 Н; г) F=6 Н; д) F=346 Н.

2. С какой скоростью нужно бросить вертикально тело с высоты 40 м, чтобы оно упало на 1 с раньше, чем в случае свободного падения?

Ответ: а) v₀=6,4 м/с; б) v₀=8,4 м/с; в) v₀=10,4 м/с; г) v₀=12,4 м/с; д) v₀=14,4 м/с.

3. Точка движется по окружности радиусом R=2 см. Зависимость пути от времени дается уравнением S=10^-3-t³. Найти полное ускорение точки в момент, когда линейная скорость точки равна v=0,3 м/с.

Ответ: а) a=5,5 м/с²; б) a=4,5 м/с²; в) a=3,5 м/с²; г) a=2,5 м/с²;

д) a=1,5 м/с².

4. Из ружья произведен выстрел строго вверх (т.е. параллельно линии отвеса). Начальная скорость пули v₀=100 м/с, географическая широта места j=60⁰. Учитывая осевое вращение Земли, определить приближенно, на сколько западнее от места выстрела упадет пуля. Сопротивление воздуха движению пули не принимать во внимание.

Ответ: а) x»0,61 м; б) x»0,41 м; в) x»0,51 м; г) x»0,21 м;

д) x»0,31 м.

5. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением e=Аt, где А=2,0×10^-2 рад/с³. Через сколько времени после начала вращения вектор полного ускорения произвольной точки тела будет составлять угол a=60⁰ с ее вектором скорости?

Ответ: а) t=8 с; б) t=7 с; в) t=5 с; г) t=9 с; д) t=3 с.

6. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями 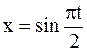, y=cospt. Найти уравнение траектории точки.

Ответ: а) y=1-x²; б) y=1+3x²; в) y=1-3x²; г) y=1+2x²; д) y=1-2x².

7. Математический маятник длиной 40 см и физический маятник в виде тонкого прямого стержня длиной 60 см (рис. 1) синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние центра тяжести стержня от оси колебаний.

Ответ: а) d₁=0,15 м; d₂=0,25 м; б) d₁=0,5 м;

d₂=0,1 м; в) d₁=0,15 м; d₂=0,15 м; г) d₁=0,2 м; d₂=0,2 м;

д) d₁=0,3 м; d₂=0,1 м.

8. На горизонтальной плоскости с коэффициентом трения m=0,10 лежит брусок массы m=0,50 кг, соединенный горизонтальной недеформированной пружиной со стенкой (рис. 2). Жесткость пружины k=2,45 Н/см, а ее масса пренебрежимо мала. Брусок сместили так, что пружинка растянулась на x₀=3,0 см, а затем отпустили. Найти число колебаний, которые совершит брусок до остановки.

Ответ: а) N=2,5; б) N=3,5; в) N=4,5; г) N=5,5; д) N=6,5.

Вариант № 15

1. Катер массой m=2 т с двигателем мощностью N=50 кВт развивает максимальную скорость v=25 м/с. Определить время t, в течение которого катер после выключения двигателя потеряет половину своей скорости. Принять, что сила сопротивления движению катера изменяется пропорционально квадрату скорости.

Ответ: а) t=3,5 с; б) t=35 с; в) t=5 с; г) t=15 с; д) t=25 с.

2. С какой скоростью нужно бросить вертикально тело с высоты 40 м, чтобы оно упало на 1 с позднее, чем в случае свободного падения?

Ответ: а) v₀=5,5 м/с; б) v₀=6,5 м/с; в) v₀=8,5 м/с; г) v₀=9,5 м/с;

д) v₀=10,5 м/с.

3. Искусственный спутник движется по окружности в плоскости земного экватора, оставаясь все время над одним и тем же пунктом земной поверхности. Определить радиус R орбиты спутника орбиты.

Ответ: а) R=52,2×10³ км; б) R=42,2×10³ км; в) R=32,2×10³ км;

г) R=22,2×10³ км; д) R=12,2×10³ км.

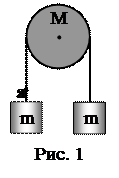4. На горизонтальную неподвижную ось насажен блок, представляющий собой сплошной цилиндр массы М=5 кг (рис. 1). Через него перекинута невесомая веревка, на концах которой висят две обезьяны массой m=20 кг каждая. Первая обезьяна начинает подниматься с ускорением а=2 м/с² относительно веревки. Определить, с каким ускорением относительно неподвижной системы координат будет двигаться вторая обезьяна.

Ответ: а) а₂=0,74 м/с²; б) а₂=0,84 м/с²; в) а₂=0,94 м/с²;

г) а₂=0,64 м/с²; д) а₂=0,54 м/с².

5. Точка А находится на ободе колеса радиусом R=0,50 м, которое катится без скольжения по горизонтальной поверхности со скоростью v=1,00 м/с. Найти модуль вектора ускорения точки А.

Ответ: а) а=2,0 м/с²; б) а=4,0 м/с²; в) а=3,0 м/с²; г) а=5,0 м/с²;

д) а=6,0 м/с².

6. Точка одновременно совершает два гармонических колебания, происходящих по взаимно перпендикулярным направлениям, и выражается уравнениями x= 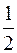sinwt, y=coswt. Найти уравнение траектории точки.

Ответ: а) y²+16x²=4; б) y²-16x²=4; в) y²+12x²=4; г) y²-12x²=4;

д) y²+10x²=4.

7. Логарифмический декремент колебаний математического маятника равен 0,2. Найти, во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника.

Ответ: а) А₀₁/А₀₂=3,22; б) А₀₁/А₀₂=2,42; в) А₀₁/А₀₂=1,42;

г) А₀₁/А₀₂=2,22; д) А₀₁/А₀₂=1,22.

8. Для определения скорости звука в воздухе методом акустического резонанса используется труба с поршнем и звуковой мембраной, закрывающей один из ее торцов (рис. 2). Найти скорость звука, если расстояние между соседними положениями поршня, при которых наблюдается резонанс на частоте n=2000 Гц, составляет l=8,5 см.

Ответ: а) v=0,34 км/с; б) v=0,37 км/с; в) v=0,38 км/с;

г) v=0,39 км/с; д) v=0,29 км/с.

Вариант № 16

1. Снаряд массой m=10 кг выпущен из зенитного орудия вертикально вверх со скоростью 800 м/с. Считая силу сопротивления воздуха пропорциональной скорости, определить время t подъема снаряда до высшей точки. Коэффициент сопротивления k=0,25кг/с.

Ответ: а) t=4 с; б) t=14 с; в) t=24 с; г) t=34 с; д) t=44 с.

2. Начальная скорость брошенного камня равна 10 м/с, а спустя 0,5 с скорость камня равна 7 м/с. На какую высоту над начальным уровнем поднимется камень?

Ответ: а) h=2 м; б) h=3 м; в) h=4 м; г) h=5 м; д) h=6 м.

3. Тело вращается равнозамедленно с начальной угловой скоростью 10 рад/с. После того как тело совершило 20 оборотов, скорость его уменьшилась до 4 рад/с. Найти угловое ускорение точки.

Ответ: а) e=-0,23 рад/с²; б) e=-0,33 рад/с²; в) e=-0,43 рад/с²;

г) e=-0,13 рад/с²; д) e=-0,53 рад/с².

4. Грузик висит на нити длиной 1 м (рис. 1). Какую минимальную начальную скорость в горизонтальном направлении следует ему сообщить, чтобы он описал окружность в вертикальной плоскости, не сходя с круговой траектории?

Ответ: а) v₀=4 м/с; б) v₀=5 м/с; в) v₀=6 м/с;

г) v₀=7 м/с; д) v₀=8 м/с.

5. Точка А находится на ободе колеса радиусом R=0,50 м, которое катится без скольжения по горизонтальной поверхности со скоростью v=1,00 м/с. Найти полный путь, проходимый точкой А между двумя последовательными моментами ее касания поверхности.

Ответ: а) S=4,0 м; б) S=6,0 м; в) S=3,0 м; г) S=4,5 м; д) S=5,0 м.

6. Складываются два колебания одинакового направления и одинакового периода x₁=sinpt и x₂=sinp(t+0,5). (Длина – в сантиметрах, время – в секундах.) Определить амплитуду А результирующего колебания.

Ответ: а) А=1,2 см; б) А=1,4 см; в) А=1,6 см; г) А=1,8 см;

д) А=2,0 см.

7. Тело массой m=4 кг, закреплённое на горизонтальной оси, совершало колебания с периодом T₁=0,8 с. Когда на эту ось был насажен диск так, что его ось совпала с осью колебаний тела, период T₂ стал равным 1,2 с. Радиус диска R=20 см, масса его равна массе тела. Найти момент инерции тела относительно оси колебаний.

Ответ: а) I_т=0,84 кг×м²; б) I_т=0,64 кг×м²; в) I_т=0,084 кг×м²;

г) I_т=0,064 кг×м²; д) I_т=0,074 кг×м².

8. Неподвижный наблюдатель воспринимает звуковые колебания от двух камертонов, один из которых приближается, а другой с такой же скоростью удаляется. При этом наблюдатель слышит биения с частотой n=2,0 Гц. Найти скорость каждого камертона, если их частота колебаний n₀= 680 Гц и скорость распространения звука в воздухе v=340 м/с.

Ответ: а) u=0,5 м/с; б) u=0,6 м/с; в) u=0,7 м/с; г) u=0,8 м/с;

д) u=0,9 м/с.

Вариант № 17

1. С вертолета, неподвижно висящего на некоторой высоте над поверхностью Земли, сброшен груз массой m=100 кг. Считая, что сила сопротивления воздуха изменяется пропорционально скорости, определить, через какой промежуток времени t ускорение a груза будет равно половине ускорения свободного падения. Коэффициент сопротивления k=10 кг/с.

Ответ: а) t=6,93 с; б) t=16,3 с; в) t=8,93 с; г) t=9,93 с; д) t=6,93 с.

2. Тело брошено под углом a₀=60⁰ к горизонту со скоростью v₀=20 м/с. Под каким углом a к горизонту будет двигаться тело через 1,5 с после начала движения (рис. 1)?

Ответ: а) a=14,7⁰; б) a=15,7⁰; в) a=16,7⁰;

г) a=17,7⁰; д) a=18,7⁰.

3. Тело вращается равнозамедленно с начальной угловой скоростью 10 рад/с. После того как тело совершило 20 оборотов, скорость его уменьшилась до 4 рад/с. Найти время, в течение которого изменилась его угловая скорость.

Ответ: а) t=18 с; б) t=15 с; в) t=12 с; г) t=21 с; д) t=14 с.

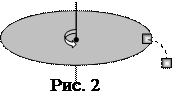4. Горизонтально расположенный диск радиусом 0,25 м вращается вокруг вертикальной оси, проходящей через центр диска (рис. 2). На диске возле его края лежит небольшой брусок. Коэффициент трения бруска по диску равен 0,2. При каком минимальном числе оборотов в минуту брусок соскользнет с диска?

Ответ: а) n=0,65 об/с; б) n=0,25 об/с; в) n=0,35 об/с;

г) n=0,45 об/с; д) n=0,55 об/с.

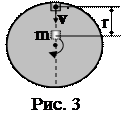5. Горизонтальный диск вращается с постоянной угловой скоростью w=60 рад/с вокруг вертикальной оси, проходящей через его центр (рис. 3). По одному из диаметров диска движется небольшое тело массы m=0,50 кг с постоянной относительно диска скоростью v^'=50 см/с. Найти силу, с которой диск действует на это тело, в момент, когда оно находится на расстоянии r=30 см от его оси вращения.

Ответ: а) F=6 Н; б) F=8 Н; в) F=4 Н; г) F=10 Н; д) F=9 Н.

6. Складываются два колебания одинакового направления и одинакового периода x₁=sinpt и x₂=sinp(t+0,5). (Длина – в сантиметрах, время – в секундах). Определить начальную фазу j_о результирующего колебания.

Ответ: а) j₀=p/2; б) j₀=p/3; в) j₀=p/4; г) j₀=p; д) j₀=p/6.

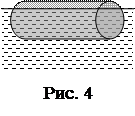7. Набухшее бревно, сечение которого постоянно по всей длине, погрузилось вертикально в воду так, что над поверхностью воды находится лишь малая (по сравнению с длиной) его часть (рис. 4). Период колебаний бревна равен 5 с. Определить длину бревна.

Ответ: а) ℓ=10,2 м; б) ℓ=8,2 м; в) ℓ=6,2 м; г) ℓ=4,2 м; д) ℓ=2,2 м.

8. Источник звуковых колебаний с частотой n₀=1700 Гц и приемник находятся в одной точке. В момент времени t₀=0 источник начинает удаляться от приемника с постоянным ускорением а=10 м/с². Считая скорость звука v=340 м/с, найти частоту колеб