Задача Д4

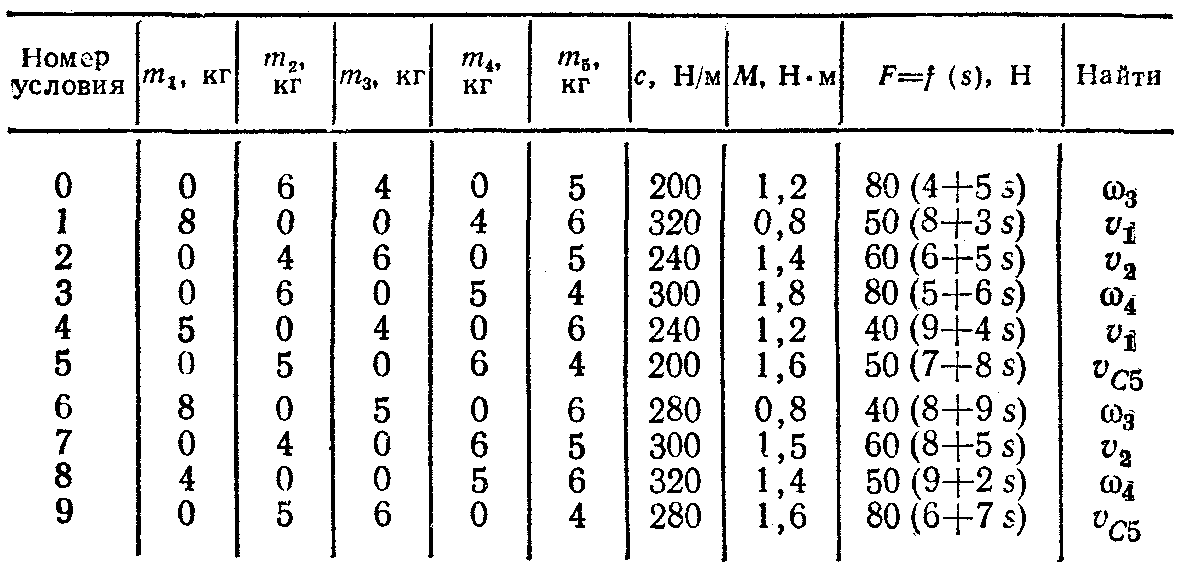
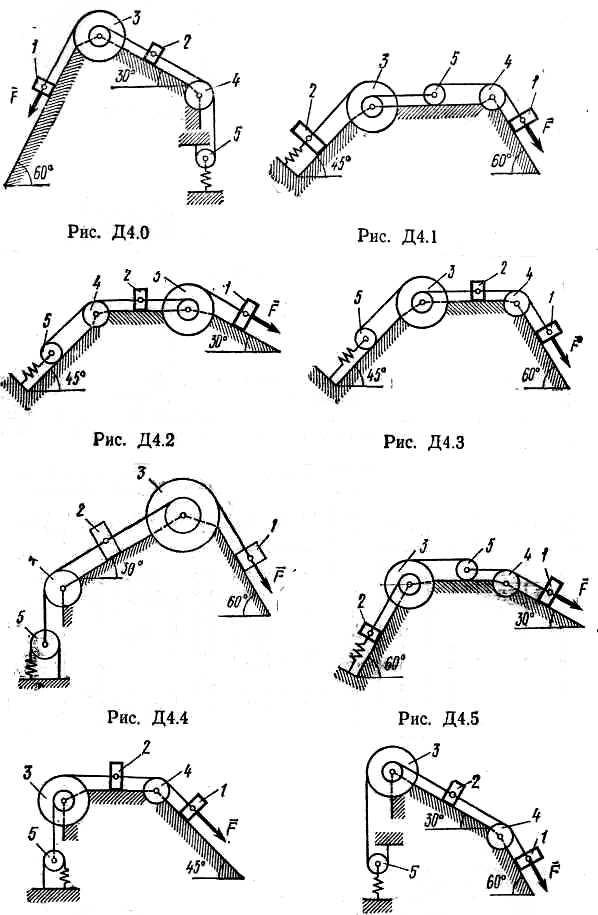
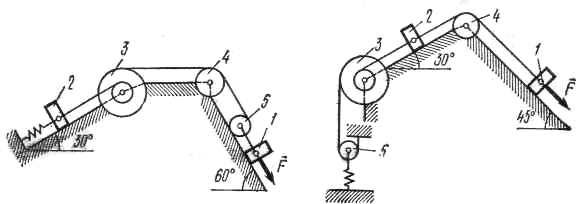
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R₃=0,3 м, r₃=0,1 м и радиусом инерции относительно оси вращения ρ₃ = 0,2 м, блока 4 радиуса R₄=0,2 м икатка (или подвижного блока) 5 (рис. Д4.0—Д4.9, табл. Д4); тело 5 считать сплошным однородным цилиндром, а массу блока 4 —равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f =0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина скоэффи­циентом жесткости с. Под действием силы F=f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопро­тивления (от трения в подшипниках).

Определить значение искомой величины в тот момент времени, когда перемещение s станет равным S₁=0,2 м. Искомая величина указана в столбце «Найти» таблицы, где обозначено: V₁, V ₂, V₃, V_c5 — скорости грузов 1, 2 и центра масс тела 5 соответственно, ω₃ и ω₄ - угловые скорости тел 3 и 4. Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 1), катятся по плоскостям без скольжения.На всех рисунках не изображать груз 2, если m₂=0; остальные тела должны изображаться и тогда, когда их масса равна нулю.

Таблица Д4

Указания. Задача Д4—на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что ки-нетическая энергия Т системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении Т для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика). При вычислении работы надо все перемещения выразить через заданное перемещение s учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями_.

Рис.Д4.4 Рис.Д4.5

Рис.Д4.2 Рис.Д4.3

Рис.Д4.0 Рис.Д4.1

Рис.Д4.6 Рис.Д4.7

Рис.Д4.8 Рис.Д4.9

Задача Д6

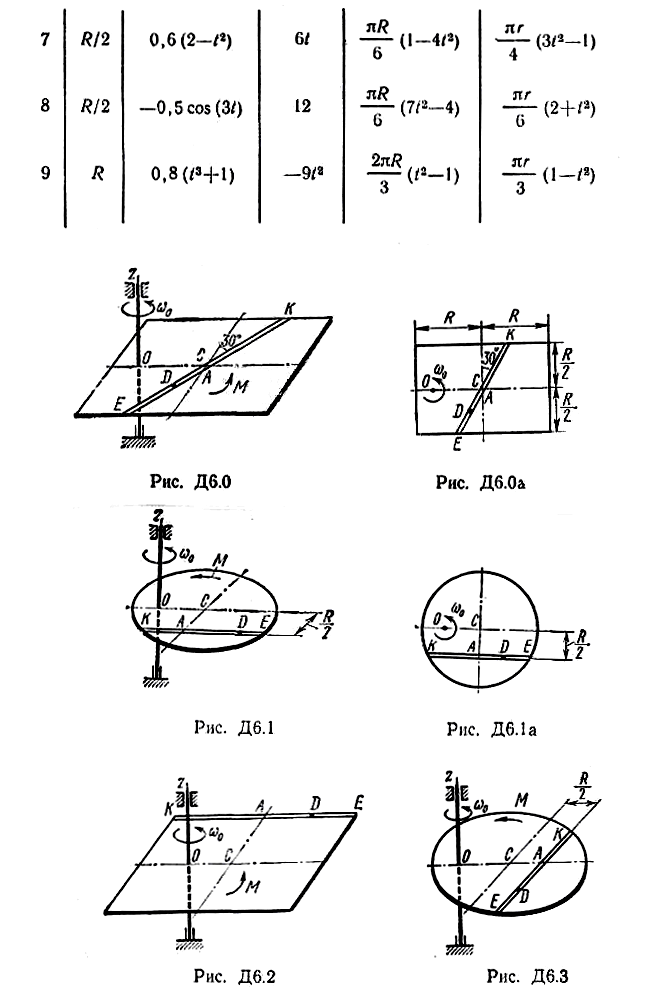
Однородная горизонтальная платформа (круглая радиуса R или прямоугольная со сторонами R и 2R, где R = 1,2 м) массой m₁ = =24 кг вращается с угловой скоростью ω₀=10 c^-1 вокруг вертикальной оси z, отстоящей от центра масс С платформы на расстоянии ОС = b (рис. Д6.0—Д6.9, табл. Д6); размеры для всех прямоугольных платформ показаны на рис. Д6.0, а (вид сверху).

В момент времени t₀ = 0 по желобу платформы начинает двигаться (под действием внутренних сил) груз D массой m₂ = 8 кг по закону s = AD = F(t), где s выражено в метрах, t — в секундах. Одновременно на платформы, изображенные на рис. О—4, начинает действовать пара сил с моментом М (задан в ньютон-метрах; при М<0 его направление противоположно показанному на рисунках); для платформ, изображенных на рис. 5—9, М = 0.

Определить: для платформ, изображенных на рис. 0—4, зависимость ω = f(t), т. е. угловую скорость платформы, как функцию времени; для платформ, изображенных на рис. 5—9, — угловую скорость ω₁ платформы в момент времени t₁ = 1 с.

Форма желоба на рис. 0—4 прямолинейная (желоб КЕ), на рис. 5, 6, 7 — окружность радиуса R (обод платформы), на рис. 8, 9 — окружность радиуса r = 0,5 R. На всех рисунках груз D показан в положении, при котором s>0 (когда s<0, груз находитсяпо другую сторону от точки А); на рис. 5—9 расстояние s = AD отсчитывается по дуге окружности. Изображая чертеж решаемой задачи, провести ось z на заданном расстоянии ОС = b от центра С.

Указания. Задача Д6 — на применение теоремы об изменении кинетического момента системы. При применении теоремы к системе, состоящей из платформы и груза, кинетический момент K_z системы относительно оси z определяется как сумма моментов платформы и груза. При этом следует учесть, что абсолютная скорость v груза складывается геометрически из относительной v_0T и переносной v_пер скоростей, т.е. v = v_0T + v_пер. Поэтому и количество движения этого груза mv = mv_от + mv_пер. Тогда можно воспользоваться теоремой Вариньона (статика),согласно которой m_z(mv) = m_z(mv_0T) +m_z(mv_nep); эти моменты вычисляются так же, как моменты сил

.В случае, когда М =0 и надо определить ω_о,необходимо воспользоваться законом сохранения кинетического момента (показав, что он здесь имеет место). При этом следует сначала найти и показать на чертеже положения D_o и D₁ груза в моменты времени (t₀ = 0 и t₁ = 1 с (найти, ему равен угол ACD при t₀ = 0 и t₁ = 1 с), а также определить, чему равна и как направлена скорость v_0T в эти моменты времени. После этого, так же как в Д6, надо вычислить K_z, но не для произвольного момента времени, а сначала для момента t₀ = 0 (когда груз в положении D_o и ω = ω ₀), а затем для момента t₁ = 1 с (когда груз в положении D₁ и ω = ω₁) и использовать закон сохранения K_z.

Момент инерции прямоугольной пластины с массой т и сторонами a₁и a₂ относительно оси Оz, перпендикулярной пластине и проходящей через ее центр масс С, равен - 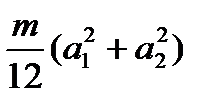.При решении задачи полезно изобразить на вспомогательном чертеже вид на платформу сверху (с конца оси z). В качестве примеров это сделано для рис.Д6.0 и Д6.1 (рис.Д6.0а,рис.Д6.1а).

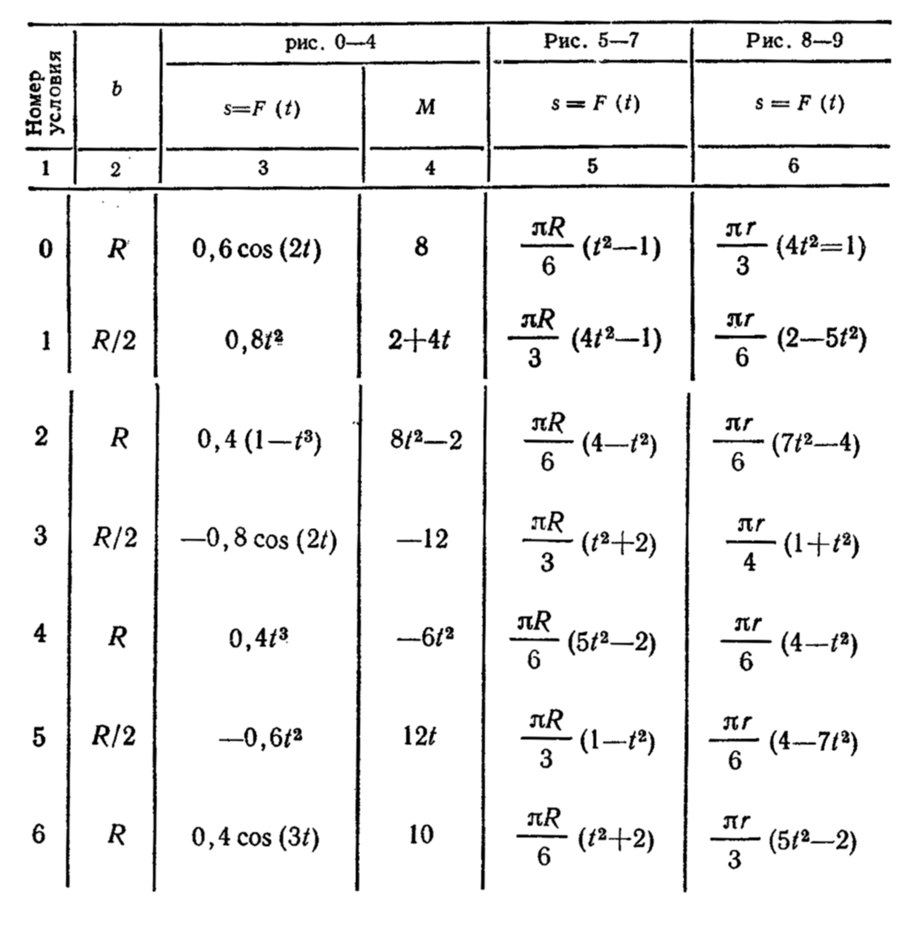Таблица Д6

Рис.Д6.0 Рис.Д6.0а

Рис.Д6.1 Рис.Д6.1а

Рис.Д6.2 Рис.Д6.3

1 2 3 4 5 6

Рис.Д6.4 Рис.Д6.5

Рис.Д6.8 Рис.Д6.9

Рис.Д6.6 Рис.Д6.7

Задача Д7

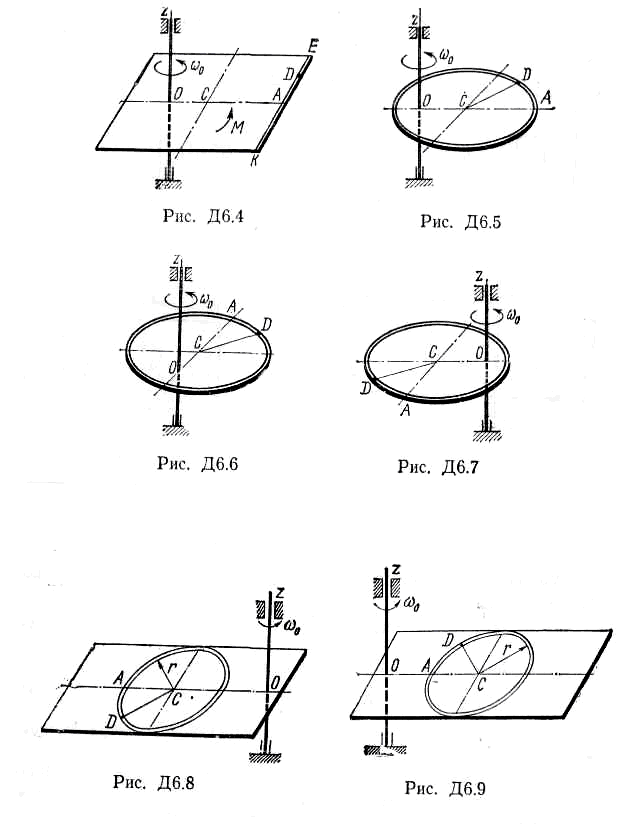
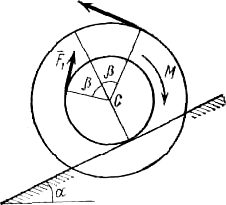
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса г = 0,6 R (рис. Д7.0—Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F₁ и F₂, направления которых определяются углом f; кроме сил на барабан действует пара с моментом М. При движении, начинающемся из состояния покоя, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона а так, как показано на рисунках.

Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. X_С = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.

Указания. Задача Д7 — на применение дифференциальных уравнений плоскопараллельного движения твердого тела. При составлении уравнений следует во избежание ошибок в знаках направить координатную ось х в ту сторону, куда предполагается направленным движение центра С барабана, и считать тогда все моменты положительными, когда они направлены в сторону вращения барабана. Если фактически направление движения центра С другое, то в ответе получится a _с<0, но найденная величина а _с будет верной. Силу трения, когда неясно, куда она направлена, можно направлять в любую сторону (результат от этого не зависит).

Таблица Д7

Определяя наименьшее значение коэффициента трения, при ко­тором возможно качение без скольжения, учесть, что сила трения не может быть больше предельной, т.е. что IF_ТРI<fN, откуда f>IF _Tp I/N. Следовательно, f_min = IF _Тр I/N. Очень существенно, что во все эти выражения входят модули сил (мы не пишем INI, так как в данной задаче не может быть N<0). Если при расчетах получится F_тр<0, то это означает лишь, что фактически сила F _ТРнаправлена в другую сторону; в остальном весь расчет будет верным.

Рис.Д7.0 Рис.Д7.1 Рис.Д7.2

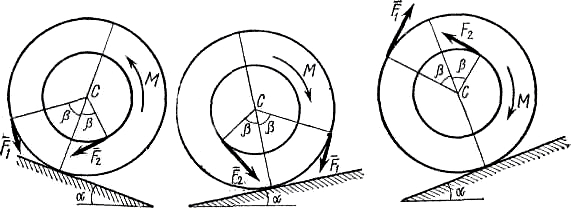
Рис.Д7.6 Рис.Д7.7

Рис.Д7.8 Рис.Д7.9

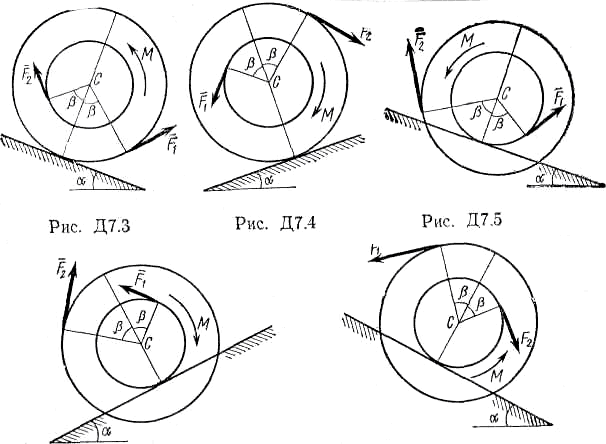
Рис.Д7.3 Рис.Д7.4 Рис.Д7.5