Ряд 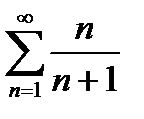 расходится по достаточному признаку расходимости, т. к.
расходится по достаточному признаку расходимости, т. к. 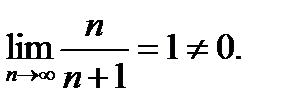
Признаки сходимости рядов с положительными членами:
1. Признак сравнения.
Пусть 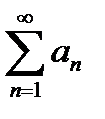 и
и 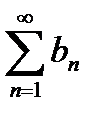 − ряды с положительными членами. Если
− ряды с положительными членами. Если
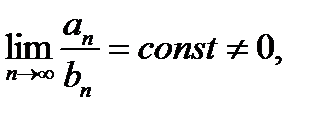
то эти ряды сходятся или расходятся одновременно.
2. Признак Даламбера. Пусть
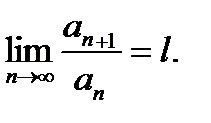
Если l < 1, то ряд 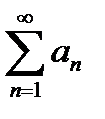 сходится.
сходится.
Если l > 1, то ряд 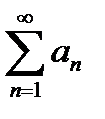 расходится.
расходится.
3. Радикальный признак Коши. Пусть
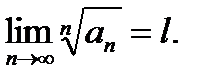
Если l < 1, то ряд 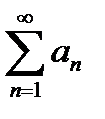 сходится.
сходится.
Если l > 1, то ряд 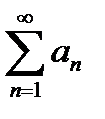 расходится.
расходится.
4. Интегральный признак Коши. Пусть f (x) − непрерывная, убывающая и положительная на промежутке [1; ∞) функция. Тогда ряд 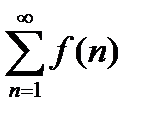 сходится (расходится), если сходится (расходится) интеграл
сходится (расходится), если сходится (расходится) интеграл
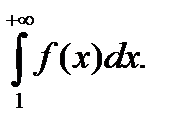
 2015-05-12
2015-05-12 485
485








