2015-05-12
2661
1.Изобразим балку с действующими на нее нагрузками (рис.15,а)
2. Изобразим оси координат x и y
3. Силу F заменяем ее составляющим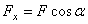и 
и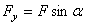 
. Равнодействующая qСD равномерно распределенной нагрузки, приложенная в точке пересечения диагоналей прямоугольника (рис.15,б), переносится по линии своего действия в середину участка CD, в точку К.
4. Освобождаем балку от опор, заменив их опорными реакциями (рис.15,в)
5. Составляем уравнения равновесия статики и определяем неизвестные реакции опор.
a) Из уравнения моментов всех действующих на балку сил, составленного относительно одной из точек опор, сразу определяем одну из неизвестных вертикальных реакций:
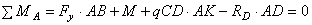
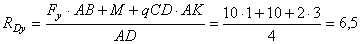кН
b) Определяем другую вертикальную реакцию:
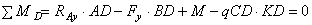
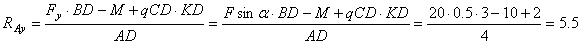кН
c) Определяем горизонтальную реакцию:
; 
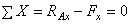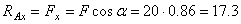кН
6. Проверяем правильность найденных результатов:
.
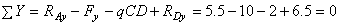Условие равновесия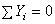 
выполняется, следовательно, реакции опор найдены верно.
Пример 2. На вал (рис.16,а) жестко насажены шкив 1 и колесо 2. Определить силы F 2, F r2=0,4F2, а также реакции опор А и В если F 1=100Н.
|
|
|
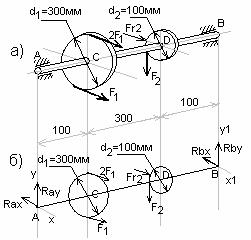
Рис.16
