Краткие теоретические сведения. Определитель – это некоторое число, поставленное в соответствие квадратной матрице

Определители

Определитель – это некоторое число, поставленное в соответствие квадратной матрице. Пусть А – произвольная квадратная матрица порядка п. Определитель матрицы А будем обозначать .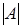

Если п=1, то матрица А состоит из одного числа А. Положим по определению, что определитель такой матрицы равен числу А, т.е. .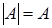

Если п=2, то матрица А имеет вид 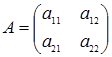. Определитель матрицы А вычисляется по формуле .

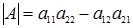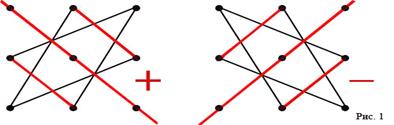
Если п=3, то матрица А имеет вид 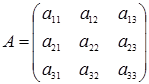. Определитель матрицы А в этом случае вычисляется по правилу треугольников (рис. 1):

.

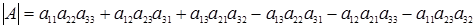Теорема Лапласа: Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) матрицы на их алгебраические дополнения. Например, разложение определителя матрицы 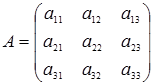по первой строке имеет вид:

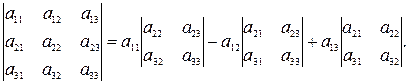
Основные свойства определителей

• Определитель не меняется при транспонировании матрицы.

• Определитель меняет знак, если поменять местами любые две строки (столбца) матрицы.

• Определитель матрицы равен нулю, если все элементы некоторой строки (столбца) равны нулю.

• Определитель матрицы равен нулю, если в этом определителе существуют две строки (два столбца), элементы которых пропорциональны, либо (в частном случае) равны.

• Определитель не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на число.