Понятие обратной матрицы вводится только для квадратных матриц. Если А – квадратная матрица, то обратной для нее матрицей называется матрица 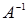 , удовлетворяющая условию
, удовлетворяющая условию 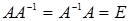 .
.
Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Если условия теоремы выполнены, то матрица обратная к матрице 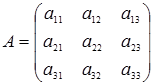 находится следующим образом:
находится следующим образом: 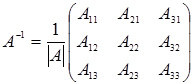 , где
, где 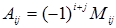 - алгебраические дополнения элементов матрицы А (
- алгебраические дополнения элементов матрицы А ( ).
). 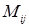 - миноры элементов матрицы А.
- миноры элементов матрицы А.
Минором 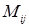 элемента
элемента 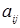 квадратной матрицы А п-го порядка называется определитель (п-1)- го порядка, полученный из определителя матрицы А вычеркиванием i-ой строки и j-го столбца.
квадратной матрицы А п-го порядка называется определитель (п-1)- го порядка, полученный из определителя матрицы А вычеркиванием i-ой строки и j-го столбца.
Аналогично для матриц второго порядка обратной будет следующая матрица: 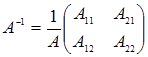
 2015-05-10
2015-05-10 272
272








