Пример 1. Найти наибольшее и наименьшее значения функции 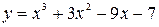 при
при 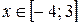 .
.
Решение.
Шаг 1. Находим область определения функции и проверяем, содержится ли в ней весь отрезок. 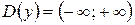 и отрезок целиком содержится в области определения.
и отрезок целиком содержится в области определения.
Шаг 2. Определяем все критические точки, попадающие в отрезок. Для этого находим производную и приравниваем ее к нулю, решаем полученное уравнение и выбираем попадающие в отрезок 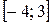 корни.
корни.
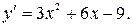
Решаем уравнение 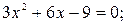
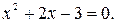
Корни уравнения 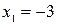 ,
, 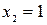 . Оба корня принадлежат отрезку
. Оба корня принадлежат отрезку 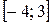 .
.
Шаг 3. Вычисляем значение функции в отобранных точках, а также на концах отрезка.
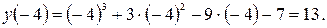
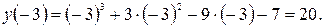
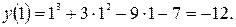
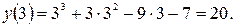
Шаг 4. Из полученных значений функции выбираем наибольшее и наименьшее значения.
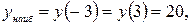
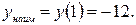
Ответ: 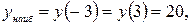
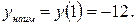
 2015-05-10
2015-05-10 742
742








