Пример 1. Найти промежутки монотонности и экстремумы функции 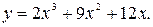

Решение.
Шаг 1. Находим область определения функции: 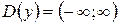 .
.
Шаг 2. Определяем все стационарные точки. Для этого находим производную и приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни.
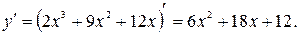
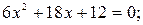
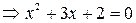 . Корни уравнения:
. Корни уравнения: 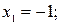
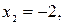 которые являются стационарными точками.
которые являются стационарными точками.
Шаг 3. Определяем все критические точки. Для этого найдем те точки, в которых производная не существует. Критических точек нет.
Шаг 4. Рисуем числовую ось, на нее наносим пустыми точки, в которых нарушается область определения, а затем закрашенными стационарные и критические точки. Эти точки разбивают числовую ось на промежутки, в каждом из которых производная сохраняет знак.
Шаг 5. Определяем знак производной на каждом из промежутков, выбирая точки из промежутков и подставляя в производную.
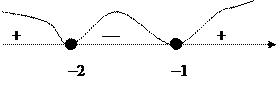
Шаг 6. Делаем выводы, используя достаточное условие экстремума и достаточное условие монотонности.
Функция убывает в интервале 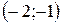 , возрастает в интервалах
, возрастает в интервалах 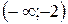 и
и 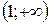 . Кроме того, в окрестностях стационарных точек
. Кроме того, в окрестностях стационарных точек 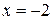 и
и 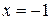 производная меняет знак, значит, они являются точками экстремума. Таким образом,
производная меняет знак, значит, они являются точками экстремума. Таким образом, 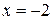 – точка максимума и
– точка максимума и 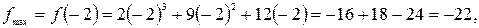
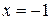 – точка минимума
– точка минимума 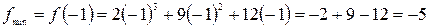 .
.
Ответ: функция убывает в интервале 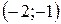 , возрастает в интервалах
, возрастает в интервалах 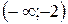 и
и 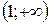 ;
; 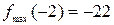 ,
, 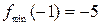 .
.
 2015-05-10
2015-05-10 18897
18897








