2015-05-10
437
Пример 1. Найти производную второго порядка функции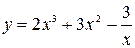 
.
Решение.
Шаг 1. Найдем первую производную функции:
.
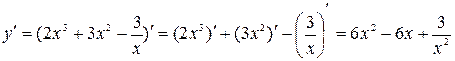Шаг 2. Найдем вторую производную
.
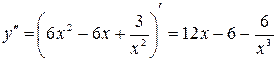Ответ: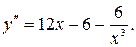 
Пример 2. Найти интервалы выпуклости и точки перегиба функции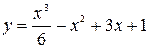 
.
Решение.
Шаг 1. Найдем первую производную функции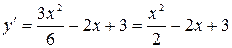 
.
Шаг 2. Найдем вторую производную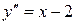 
.
Шаг 3. Решим уравнение: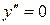 
. 
, 
.
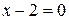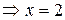Шаг 4. Исследуем знак второй производной слева и справа от полученной точки:
| Промежуток |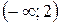 
| 
|
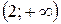
Знак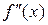 
| – | + |
| Направление выпуклости | Ç | È |
Так как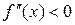 
на промежутке 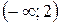, то функция выпукла на этом промежутке. На промежутке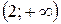 
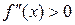, следовательно, функция вогнута на 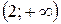. Так как при переходе через точку 
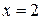вторая производная изменяет свой знак, то 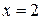– точка перегиба.
Найдем значение функции в точке перегиба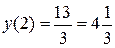 
.
Ответ: функция выпукла на 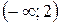, вогнута на 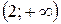, 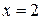– точка перегиба.
