Краткие теоретические сведения. Производной второго порядка функции называется производная от производной первого порядка, т

Производной второго порядка функции 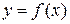называется производная от производной первого порядка, т. е. 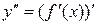. Аналогично, производной п-го порядка функции 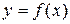называется производная от производной (п-1)-го порядка, т. е. .

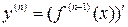Теорема. Если функции 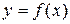во всех точках интервала 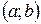имеет отрицательную вторую производную, т.е. 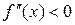, то функция выпукла на 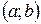. Если же 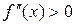для любого 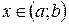, то функция вогнута на интервале .

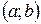Теорема (достаточное условие существования точек перегиба). Если вторая производная 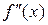при переходе через точку 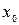, в которой она равна нулю или не существует, меняет знак, то точка графика функции 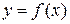с абсциссой 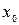есть точка перегиба.

Теорема. Если в точке 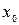первая производная функции 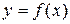равна нулю, а вторая производная в точке 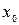существует и отлична от нуля, то при 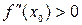в точке 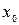функция имеет минимум, а при 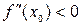в точке 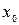функция имеет максимум.