Методические указания по выполнению третьего задания

Для несущих конструкций знакопеременная сила вызывает, как правило, знакопеременную деформацию, величина, равная полусумме наибольшего σ_max и наименьшего σ_min напряжений называют средним σ_ср= 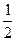(σ_max + σ_min) При создании вибропрочной конструк­ции РЭС прочность определяется не по статической, а по цикли­ческой нагрузке. Циклической прочностью считают способность ма­териала выдерживать знакопеременную нагрузку в течение опреде­ленного количества циклов. Это вызывает наступление усталости материала. При такой нагрузке металлы разрушаются при напря­жениях меньших предела статической нагрузки. И наоборот, усталостного явления не наблюдается, если циклическое натяжение равно или меньше предела усталостной прочности. Пределом уста­лости материала является напряжение σ_у 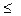σ_ср , которое матери­ал в состоянии выдерживать при данном

числе циклов.

Для симмет­ричного знакопеременного цикла существуют соотношения между пределом усталости на изгиб σ_упр пределом прочности σ_пр и условным пределом текучести σ_тек.

Для стали

σ_упр = 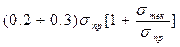, (27)

для алюминиевых и магниевых сплавов

σ_упр = 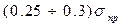, (28)

для медных сплавов

σ_упр = 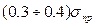, (29)

В сравнении с симметричным знакопеременным изгибом предел усталости на растяжение или сжатие больше в 1,1 - 1,5 раза, а на кручение - меньше в 1,5 - 2 раза. Знакопеременные напряжения вли­яют на собственную частоту балочной конструкции (рис. 8) 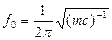, где 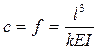- величина обратная жест­кости, и вибропрочность при знакопеременном напряжении характе­ризуется отношением Е/γ.

При большем Е/γ будет выше вибропрочность и собственная частота конструкции РЭС. Для заданной стержневой конструкции длиной l (Тип зада­ется преподавателем) рассчитать собственную частоту при консольном закрепления балки. Измерить частоту и прогиб для консольно-закрепленного стержня на вибрационной установке ВС-68.

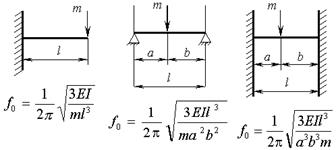
а) б) в)

Рис. 8. Виды закреплений стержневых конструкций

Изменяя частотно-модулированный сигнал с вибростенда, добиться максимальной деформации балки при знакопеременном напряжении, амплитуде основания вибростенда измеряется по методу клина и не превыша­ет S_a 2 мм. Результаты измерений стрелы прогиба и частоты колебаний конструкции занести в отчет. Определить предел уста­лости балки для заданного материала.

Задание четвертое. Определить стрелу прогиба и толщину бор­тового герметичного стального корпуса при давлении р = 0,098 Мпа.

Методические указания по выполнению четвертого задания.

Для защиты влаги многие корпуса радиоаппаратуры герметизи­руют. Герметичные корпуса бывают цилиндрической формы и в виде, параллелепипеда, у которого стенки и дно выполняются прямоугольными (рис. 9). Герметичные корпуса блоков бортовой РЭА при подъеме на вы­соту подвергаются воздействию внутреннего избыточного давления, в результате стенки начинают деформироваться (выпучиваться). Аналогично происходит с герметичными корпусами при погружении ихна глубину,

при этом стенки деформируются только во внутрь корпуса.

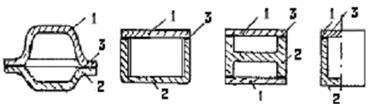
Рис. 9. Различные варианты конструкций РЭС (I - крышка; 2 - корпус; 3 - уплотнительный стык)

Рассмотрим напряжения и деформаций, которые возникают в герметичных корпусах бортовой РЭА при подъеме их на высоту.

Принимая каждую боковину и дно корпуса, имеющего форму паралле­лепипеда, как прямоугольную пластинку, защемленную по контуру, напряжение σ _и (Мпа) на контуре в середине длинной опоры а_K (а_K >в_к) /5/

σ _и = С₁ p(в/h)². (30)

Прогиб f_u (в мм) в центре боковинки или дна

F_u = C₂ p в⁴ / Е h³,

где p - внутреннее давление, МПа;

h - толщина стенки или дна, мм;

Е - модуль упругости материала, МПа.

Коэффициенты C₁ и С₂ в зависимости от отношения а/в при­ведены в приложении (табл. 2). Корпус бортового РЭС имеет раз­меры а_к - 420 мм, в_к = 300 мм, h_k = 300 мм, изготавливают из алюминиевого сплава с Е = 70000 МПа. Считая σ _и = в 200 МПа, определить толщину крышки h и стрелу прогиба - f_u

5. УКАЗАНИЯ ПО ОФОРМЛЕНИЮ ОТЧЕТА

Отчет оформляется в соответствии с требованиями, изложенными в методических указаниях к лабораторной ра­боте № I.

6. КОНТРОЛЬШЕ ВОПРОСЫ К ЛАБОРАТОРНЫМ ЗАДАНИЯМ

1. Как определяются толщина и прогиб бортового блока РЭС?

2. Почему деформацию изгиба несущих конструкций РЭС заменяют деформацией растяжения - сжатия?

3. Каким образом зависят момент инерции и момент сопротив­ления несущей конструкции с ребрами жесткости от относительной высоты и ширины ребра?

4. Чем повышают оптимальную жесткость листовых деталей?

5. Как связан предел усталости на изгиб с пределом прочности деталей?

6. Как влияет жесткость на частоту колебаний простейших балочных конструкций?

7. От чего зависит выбор конструкционных материалов, работающих на изгиб?

8. Запишите условие прочности при изгибе балочных конструкций.

9. Для каких способов закрепления балочных конструкций характерен максимальный коэффициент жесткости?

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Андреев А.И. Прикладная механика/ И.В. Андреев. Воронеж, ВГТУ, 2008. 180 с.

2. Иосилевич Г.В. Прикладная механика/ Г.В. Иосилевич, Г.Б. Строганов, Г.С. Маслов. М.: Высш. шк., 1989. 381 с.

3. Красковский Е.Я. Расчет и конструирование механизмов приборов и вычислительных систем/ Е.Я. Красковский, Ю.А. Дружинин, Е.М. Филатова. М.: Высш. шк.. 1991. 480 с.

4. Поляков К.П. Конструирование приборов и устройств радио­электронной аппаратуры / К.П. Поляков. М.: Радио и связь, 1982. 240 с.

5. Овcищер П. И. Несущие конструкции радиоэлектронной аппаратуры/ П. И. Овсищер, Ю В. Голованов, В. П. Ковешников и др. Под ред. Овсищера П.И. М.: Радио и связь, 1988. 232 с.

ПРИЛОЖЕНИЕ

Таблица 1