Прямая на плоскости.
Краткие теоретические сведения.
|
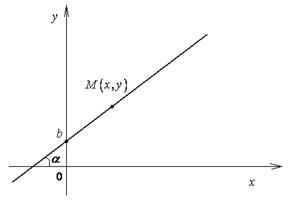
Уравнение прямой с угловым коэффициентом k:
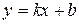 , где
, где 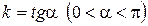 . (1)
. (1)
Если k = 0, то прямая y = b параллельно оси О х.
Если 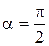 , то
, то 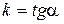 не существует и прямая х = а параллельна оси О у.
не существует и прямая х = а параллельна оси О у.
Уравнение прямой, проходящей через две данные точки 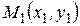 и
и 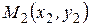 .
.
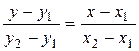 . (2)
. (2)
Общее уравнение прямой на плоскости
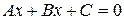 , (3)
, (3)
где А, В, С – числовые коэффициенты, причем 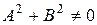 .
.
Условие параллельности и перпендикулярности прямых.
Пусть заданы две прямые
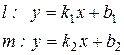
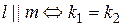 . (4)
. (4)
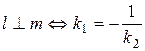 . (5)
. (5)
Решение типовых заданий.
Задание 1: составить уравнение прямой, проходящей через точку А (3;-2):
а) под углом 135° к оси О х; б) параллельно оси О у; в) параллельно оси О х.
Решение:
Шаг 1: найти угловой коэффициент прямой:
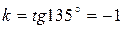 .
.
Шаг 2: подставить значение углового коэффициента в уравнение прямой (1):
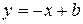 (*)
(*)
Шаг 3: подставить в уравнение прямой (*) точку, через которую проходит прямая и выразить значение b
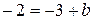
b =1
Шаг 4: подставить значение b в уравнение прямой (*):
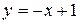 .
.
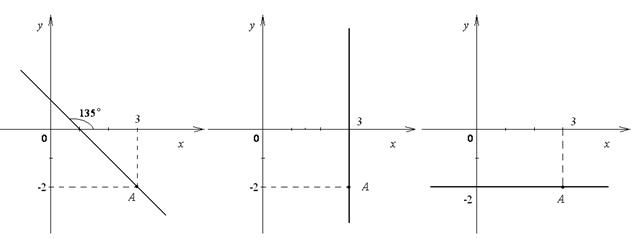
б) Уравнение прямой, проходящей через т. А (3;-2) параллельно оси О у, имеет вид х =3.
|
в) Уравнение прямой, проходящей через т. А (3;-2) параллельно оси О х, имеет вид у =-2.
а) б) в)
Ответ: а) у=-х+ 1; б) х =3. в) у =-2.
Задание 2: Составить уравнение прямой, проходящей через точки А (-5; 4) и B (3;-2):
Решение:
Шаг 1: Подставим точки А и В в уравнение прямой (2):
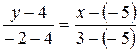
Шаг 2: Выразить у через х:
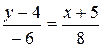
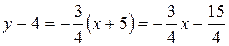
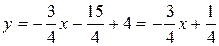
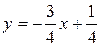
Ответ: 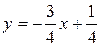 .
.
Задание 3: Составить уравнение прямых, проходящих через точку пересечения прямых 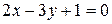 и
и 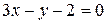 параллельно и перпендикулярно прямой
параллельно и перпендикулярно прямой 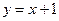 .
.
Решение:
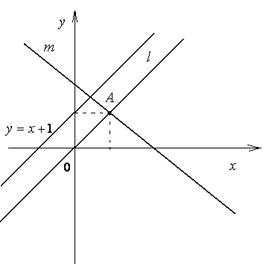
Шаг 1: Найти точку пересечения двух прямых, решив систему уравнений:
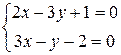
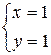
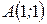 .
.
Шаг 2: Определить угловой коэффициент прямой 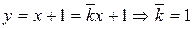 .
.
Шаг 3: найти угловые коэффициенты прямых параллельных и перпендикулярных прямой 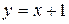 по формулам (4), (5):
по формулам (4), (5):
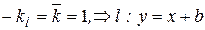
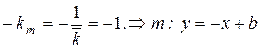
Шаг 4: подставить т. А в уравнения прямых параллельных и перпендикулярных прямой 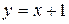 и найти значения b:
и найти значения b:
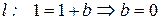
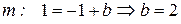 .
.
|
Шаг 5: по формуле (1) написать уравнения искомых прямых
- прямая l параллельна прямой 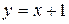 :
:
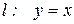
- прямая m параллельна прямой 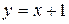 :
:
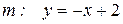 .
.
 2015-05-10
2015-05-10 340
340








