Пусть функция 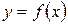 интегрируема на отрезке
интегрируема на отрезке 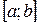
Теорема (Формула Ньютона-Лейбница). Если 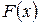 – первообразная функции
– первообразная функции 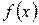 на
на 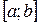 , то
, то 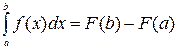 .
.
Теорема (замена переменной в определенном интеграле). Если
1) функция  и ее производная
и ее производная 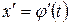 непрерывны при
непрерывны при 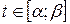 ;
;
2) множеством значений функции  при
при 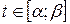 является отрезок
является отрезок 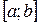 ;
;
3) 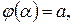
 , то
, то 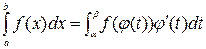 .
.
Интегрирование по частям в определенном интеграле осуществляется с помощью формулы: 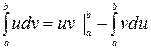 .
.
Некоторые свойства определенного интеграла
1. При перестановке пределов интегрирования определённый интеграл меняет знак на противоположный 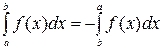 .
.
2. Постоянный множитель можно вынести за знак определённого интеграла, т.е. 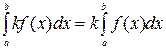 .
.
3. Определённый интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т.е. 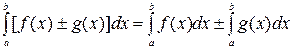 .
.
 2015-05-10
2015-05-10 228
228








