Решение типовых заданий. Задание 1. Найти линейную комбинацию векторов

Задание 1. Найти линейную комбинацию 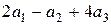векторов , , .

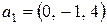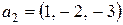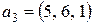Решение:

Найдем векторы

,

.

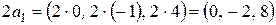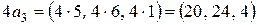Теперь получаем

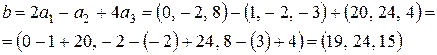
Задание 2. Выяснить, являются ли следующие векторы линейно зависимыми или линейно независимыми:

а) ,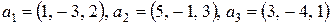

б) .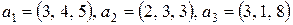

Решение:

а) Шаг 1. составить векторное равенство (2):

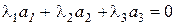или

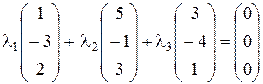
Шаг 2. составить равносильную систему уравнений:

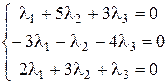
И решить ее методом Гаусса:

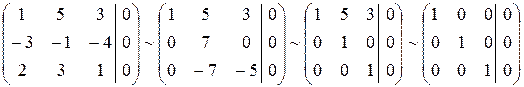
Система уравнений имеет единственное решение .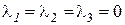

Шаг 3. Т.к. системе уравнений имеет единственное нулевое решение, то векторы по определению (2) линейно независимы.

б) Шаг 1. составим векторное равенство (2)

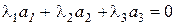или .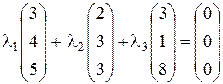

Шаг 2. Составим равносильную систему линейных уравнений

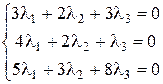и решим ее методом Гаусса:

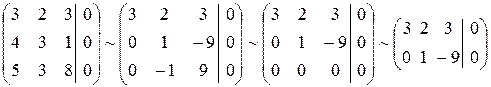
Т.к. у полученной ступенчатой матрицы число строк 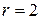меньше числа неизвестных в системе 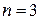, то система имеет бесконечное множество решений, в т.ч. ненулевых.

Шаг 3. Т.к. векторное уравнение (2) имеет ненулевое решение 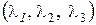, то векторы линейно зависимы.