УЧЕБНАЯ ДИСЦИПЛИНА – «Дифференциальные уравнения».
Часть 3. Системы дифференциальных уравнений.
ЗАНЯТИЕ 13. Системы дифференциальных уравнений в нормальной форме. Понятие общего решения. Задача Коши для системы. Решение системы сведением к одному ДУ более высокого порядка.
| Ауд. | Л-4. Гл. 10 | № 412, 414, 416, 418, 420, 422*, 427 + 431, 432, 438, 440, 444. | 7+5 |
☺ ☻ ☺
Общие сведения. Учитывая, что в предлагаемых для самостоятельных упражнений заданиях мы ограничиваемся системами, состоящими из двух уравнений, все общие выражения относим только к системам двух дифференциальных уравнений: 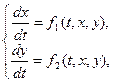 (1)
(1)
где функции 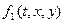 ,
, 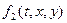 – заданные, дифференцируемые.
– заданные, дифференцируемые.
Замечание: при ссылках на отдельные уравнения системы будем использовать двухпозиционные записи; например: (1.1) – ссылка на 1-е уравнение системы (1).
1). Продифференцируем уравнения (1.1) и (1.2) системы (1) по 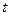 , учитывая, что
, учитывая, что 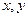 – некоторые функции независимой переменной
– некоторые функции независимой переменной 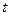 :
: 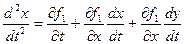 . (2)
. (2)
Воспользовавшись уравнениями (1.1) и (1.2), запишем выражение (2) в виде:
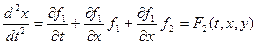 . (3)
. (3)
2). Из выражений (1.1) и (3) составим систему уравнений: 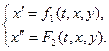 (4)
(4)
|
|
|
Для удобства, в системе уравнений (4) принято: 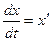 ,
, 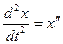 . Применяя общие правила решения системы уравнений, выразим (считая, что это возможно!) из уравнения (4.1) функцию
. Применяя общие правила решения системы уравнений, выразим (считая, что это возможно!) из уравнения (4.1) функцию 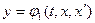 и подставим её в уравнение (4.2):
и подставим её в уравнение (4.2):
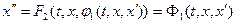 . (5)
. (5)
3). Уравнение (5) – дифференциальное уравнение 2-го порядка для функции 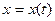 . Решая это уравнение, получим:
. Решая это уравнение, получим: 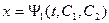 , (6)
, (6)
где  ,
,  – произвольные постоянные. Используя решение
– произвольные постоянные. Используя решение 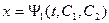 , вычисляем
, вычисляем 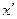 и записываем:
и записываем: 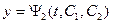 .
.
4). Используя решения 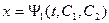 и
и 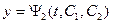 , оформляем общее решение исходной системы (1).
, оформляем общее решение исходной системы (1).
••• ≡ •••
Пример 1 – 412: Решить систему уравнений: 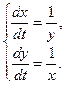 (1)
(1)
Решение:
Замечание: система уравнений не является линейной, применим метод сведения системы уравнений к одному уравнению 2-го порядка относительно 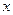 или
или 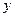 .
.
1). Продифференцируем по t уравнение (1.1): 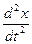 =–
=– 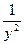
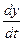 , учтём (1.2) →
, учтём (1.2) → 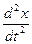 =–
=– 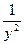
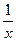 . Далее учитываем из (1.1):
. Далее учитываем из (1.1): 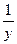 =
= 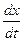 , после чего получаем уравнение:
, после чего получаем уравнение: 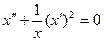 , или
, или 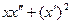 . Последнее равносильно уравнению
. Последнее равносильно уравнению 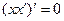 .
.
2). Интегрируя уравнение 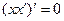 , получаем:
, получаем: 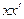 =
= 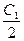 , или
, или 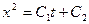 .
.
3). Учитывая уравнение (1.1), из выражения 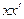 =
= 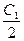 получаем:
получаем: 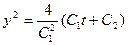 .
.
4). Общее решение записывается в виде системы: 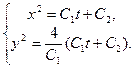 .
.
Ответ: общее решение системы: 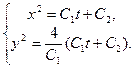 .
.
Пример 2 – 414: Решить систему уравнений: 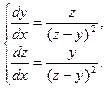 (1)
(1)
Решение:
1). Умножив (1.1) на 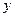 и учитывая (1.2), получим:
и учитывая (1.2), получим: 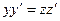 . Интегрируя последнее, легко получаем:
. Интегрируя последнее, легко получаем: 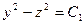 .
.
2). Перепишем (1.1), применяя тождественные преобразования: 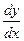 =
= 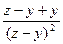 =
= 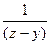 +
+ 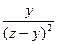 . Учитывая (1.2), запишем:
. Учитывая (1.2), запишем: 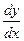 =
= 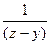 +
+ 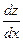 , или
, или 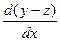 =–
=– 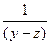 . Последнее уравнение легко интегрируется (если иметь в виду
. Последнее уравнение легко интегрируется (если иметь в виду 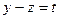 ):
): 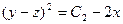 .
.
3). Используя выражения 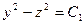 и
и 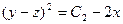 , легко получить (сложив эти выражения!):
, легко получить (сложив эти выражения!): 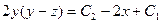 . Модифицируя постоянные:
. Модифицируя постоянные:  → 2
→ 2  ;
;  → 2
→ 2  , запишем:
, запишем: 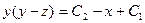 . Возводя последнее выражение в квадрат, и учитывая выражение
. Возводя последнее выражение в квадрат, и учитывая выражение 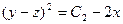 , получим:
, получим: 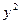 =
= 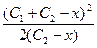 . Используя
. Используя 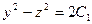 , нетрудно получить
, нетрудно получить 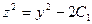 =
= 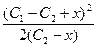 .
.
Замечание: Пример хорошо иллюстрирует возможности импровизации при решении системы ДУ применением метода сведения системы к одному уравнению высшего порядка.
|
|
|
Ответ: общее решение системы: 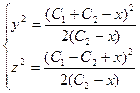 .
.
Пример 3 – 416: Решить систему уравнений: 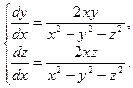 (1)
(1)
Решение:
1). Из уравнения (1.1) получим: 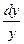 =
= 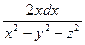 , аналогично из (1.2):
, аналогично из (1.2): 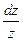 =
= 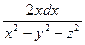 . Эти два выражения дают:
. Эти два выражения дают: 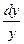 =
= 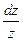 →
→ 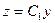 .
.
2). Учитывая 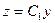 , перепишем (1.1):
, перепишем (1.1): 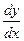 =
= 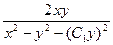 →
→ 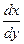 =
= 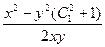 . Или в виде:
. Или в виде: 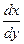 =
= 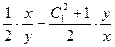 – однородное уравнение в стандартной форме. Его стандартное решение даёт:
– однородное уравнение в стандартной форме. Его стандартное решение даёт: 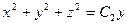 . Замечание: проверка условия:
. Замечание: проверка условия: 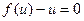 здесь не нужна из-за участия произвольной постоянной величины
здесь не нужна из-за участия произвольной постоянной величины  .
.
Ответ: общее решение системы: 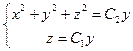 .
.
Пример 4 – 418: Решить систему уравнений: 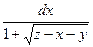 =
= 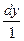 =
= 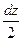 (1)
(1)
Решение:
1). Из уравнения: 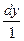 =
= 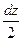 получаем:
получаем: 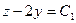 . Учитывая полученное выражение, запишем уравнение:
. Учитывая полученное выражение, запишем уравнение: 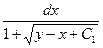 =
= 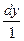 или:
или: 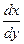 =1+
=1+ 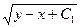 .
.
2). Полученное уравнение стандартным алгоритмом приводится к уравнению с разделяющимися переменными! Пусть: 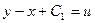 , вычислим производную по переменной
, вычислим производную по переменной 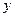 , имеем:
, имеем: 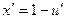 . Тогда
. Тогда 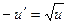 , окончательно:
, окончательно: 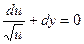 – переменные разделились! Интегрируя последнее, получаем выражение:
– переменные разделились! Интегрируя последнее, получаем выражение: 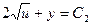 , или
, или 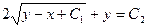 .
.
Ответ: общее решение системы: 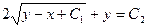 ,
, 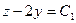 .
.
Пример 5 – 420: Найти общее и частное решения: 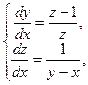
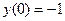 ,
, 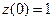 . (1)
. (1)
Решение:
1). Продифференцируем уравнение (1.2): 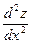 =–
=– 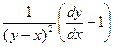 =
= 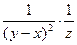 . Учитывая уравнение (1.2) получим уравнение:
. Учитывая уравнение (1.2) получим уравнение: 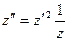 , которое не содержит переменной
, которое не содержит переменной 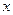 и решается понижением порядка.
и решается понижением порядка. 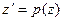 →
→ 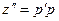 . Тогда имеем:
. Тогда имеем: 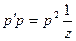 , или (так как из уравнения (1.2):
, или (так как из уравнения (1.2): 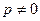 ) уравнение:
) уравнение: 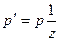 – уравнение с разделяющимися переменными, откуда:
– уравнение с разделяющимися переменными, откуда: 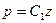 и далее выражение:
и далее выражение: 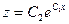 .
.
2). Дифференцируем выражение: 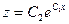 и используем уравнение (1.2). Полученное выражение для функции
и используем уравнение (1.2). Полученное выражение для функции 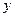 :
: 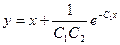 .
.
3). Общее решение уравнения: 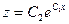 ,
, 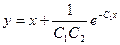 .
.
4). Используя заданные начальные условия, имеем: 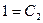 ,
, 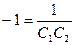 , откуда получаем величины
, откуда получаем величины 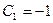 ,
, 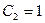 . Записываем частное решение:
. Записываем частное решение: 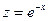 ,
, 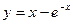 .
.
Ответ: Частное решение: 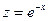 ,
, 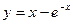 .
.
Пример 6 – 422*: Для системы уравнений: 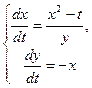 и функций
и функций 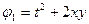 и
и 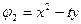 .
.
проверить, являются ли соотношения 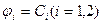 первыми интегралами системы.
первыми интегралами системы.
Решение:
Замечание: 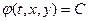 является первым интегралом системы
является первым интегралом системы 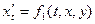 ,
, 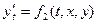 тогда и только тогда, когда:
тогда и только тогда, когда: 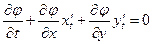 . (1)
. (1)
1). Проверим уравнение (1) для функции 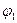 :
: 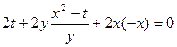 – тождественно. Является.
– тождественно. Является.
2). Проверим уравнение (1) для функции 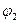 :
: 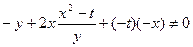 . Не является.
. Не является.
Ответ: соотношение 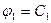 – является, а соотношение
– является, а соотношение 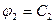 – не является.
– не является.
Пример 7 – 427: Решить систему уравнений: 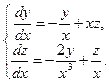 (1).
(1).
Решение:
1). Перепишем уравнение (1.1): 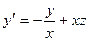 →
→ 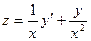 . Для дальнейшего использования уравнение (1.2) запишем в виде:
. Для дальнейшего использования уравнение (1.2) запишем в виде: 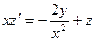 .
.
2). Продифференцируем уравнение (1.1): 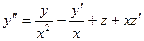 . Учитывая выражения для функции
. Учитывая выражения для функции 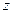 и для произведения
и для произведения 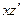 , получим уравнение
, получим уравнение 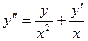 , которое после умножения на
, которое после умножения на 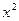 . принимает вид:
. принимает вид: 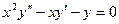 – уравнение Эйлера. (2)
– уравнение Эйлера. (2)
3). Применим подстановку: 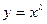 .Вычисляя производные
.Вычисляя производные 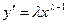 ,
, 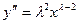 и учитывая уравнение (2), получаем уравнение:
и учитывая уравнение (2), получаем уравнение: 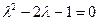 . Его корни:
. Его корни: 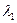 =
= 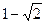 ,
, 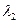 =
= 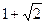 .
.
4). Записываем ФСР: 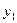 =
= 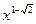 и
и 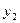 =
= 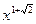 . Общее решение:
. Общее решение: 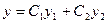 =
= 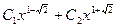 .
.
5). Вычислим производную: 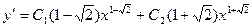 . Учитывая полученное ранее выражение
. Учитывая полученное ранее выражение 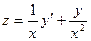 , получаем:
, получаем: 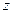 =
= 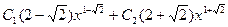 .
.
Ответ: общее решение системы 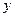 =
= 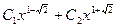 ;
; 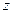 =
= 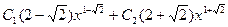 .
.
Замечание: обратим внимание на особенности применения способа решения системы ДУ сведением к уравнению высшего порядка для одной из искомых функций: здесь интенсивное применение средств математического анализа сочетается с достаточно тонкими средствами школьной алгебры!..
F☺☺E
Общие сведения. Учитывая, что трудоёмкость решения систем дифференциальных уравнений существенно зависит от числа функций, участвующих в построении системы, в предлагаемых для самостоятельных упражнений заданиях мы ограничиваемся системами, состоящими из двух уравнений. Поэтому все общие выражения, применяемые при решении систем уравнений, относим только к системам двух дифференциальных уравнений: 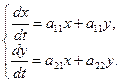 (1)
(1)
где 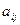 – действительные числа (постоянные);
– действительные числа (постоянные); 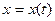 ,
, 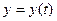 – искомые, дифференцируемые функции.
– искомые, дифференцируемые функции.
Замечание: при ссылках на отдельные уравнения системы будем использовать двухпозиционные записи; например: (1.1) – ссылка на 1-е уравнение системы (1).
☻
1. Что такое «нормальная форма» записи системы уравнений 1-го порядка?
2. Как уравнение n-го порядка представить в виде системы уравнений 1-го порядка?
3. Как систему уравнений 1-го порядка сводят к одному уравнению n -го порядка?
|
|
|
4. Как записывают начальные условия для системы трёх уравнений 1-го порядка?
F☺☺E
Общие сведения. Учитывая, что трудоёмкость решения систем дифференциальных уравнений существенно зависит от числа функций, участвующих в построении системы, в предлагаемых для самостоятельных упражнений заданиях мы ограничиваемся системами, состоящими из двух уравнений. Поэтому все общие выражения, применяемые при решении систем уравнений, относим только к системам двух дифференциальных уравнений: 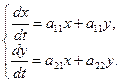 (1)
(1)
где 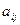 – действительные числа (постоянные);
– действительные числа (постоянные); 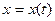 ,
, 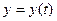 – искомые, дифференцируемые функции.
– искомые, дифференцируемые функции.
Замечание: при ссылках на отдельные уравнения системы будем использовать двухпозиционные записи; например: (1.1) – ссылка на 1-е уравнение системы (1).
Решение системы уравнений подсказывает равносильность системы (1) линейному дифференциальному уравнению 2-го порядка с постоянными коэффициентами для любой из функций 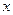 ,
, 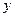 , а также свойство производной функции
, а также свойство производной функции 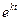 : при дифференцировании вид функции не меняется. Так как в системе уравнений участие функций
: при дифференцировании вид функции не меняется. Так как в системе уравнений участие функций 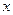 ,
, 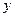 согласовывается при помощи коэффициентов
согласовывается при помощи коэффициентов 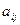 , то, нетрудно догадаться, что решение системы следует искать в виде:
, то, нетрудно догадаться, что решение системы следует искать в виде: 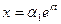 ,
, 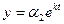 , (2)
, (2)
причем коэффициенты 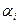 ,
, 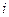 =1,2 – будут определяться из условия, что совокупность функций в записи (2) есть решение системы уравнений (1):
=1,2 – будут определяться из условия, что совокупность функций в записи (2) есть решение системы уравнений (1):
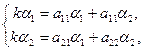 или
или 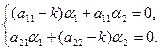 (3)
(3)
Замечание: система уравнений (3) записана с учётом деления каждого из уравнений на общий множитель: 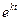 .
.
Известно, система линейных однородных (алгебраических) уравнений имеет ненулевые решения только в случае, если её определитель равен нулю:
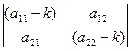 =
= 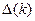 =0. (4)
=0. (4)
Уравнение-многочлен 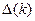 =0 называется характеристическим для системы (1), его корни – характеристическими корнями этой системы.
=0 называется характеристическим для системы (1), его корни – характеристическими корнями этой системы.
Дальнейшее использование полученных характеристических корней зависит от их вида. Различают случаи:
Случай -1. Корни уравнения ∆(k) = 0 действительные и различные: 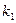 ,
, 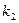 .
.
Для каждого 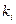 из системы (3) определится набор коэффициентов:
из системы (3) определится набор коэффициентов: 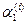 ,
, 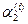 ,
, 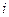 =1,2, что определит полный набор решений системы (1):
=1,2, что определит полный набор решений системы (1):
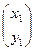 =
= 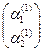 ·
· 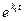 ,
, 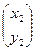 =
= 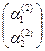 ·
· 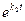 , (5)
, (5)
Учитывая теорему: сумма решений однородной системы уравнений – тоже решение, можем записать общее решение системы уравнений (1):
|
|
|
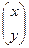 =
=  ·
· 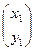 +
+  ·
· 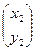 =
=  ·
· 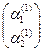 ·
· 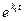 +
+  ·
· 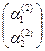 ·
· 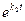 , (6)
, (6)
где  ,
,  - произвольные постоянные. Запись (6) называют общим решением системы уравнений (1).
- произвольные постоянные. Запись (6) называют общим решением системы уравнений (1).
Если заданы начальные условия: 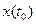 =
= 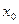 ,
, 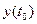 =
= 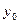 , можно определить такие значения
, можно определить такие значения  ,
,  , что из множества интегральных кривых будет выделена та, которая проходит через точку
, что из множества интегральных кривых будет выделена та, которая проходит через точку 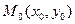 .
.
Случай -2. Корни уравнения ∆(k) = 0 комплексные: 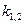 =
= 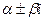 .
.
Для пары корней 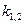 из системы (3) определятся:
из системы (3) определятся: 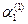 =
= 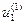
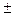 i
i 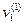 ;
; 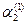 =
= 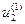
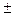 i
i 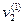 . Применим сначала знак
. Применим сначала знак 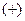 , запишем решение системы (1):
, запишем решение системы (1):
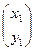 =
= 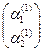 ·
· 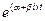 =
= 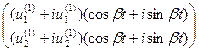 ·
· 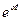 , (7)
, (7)
после выполнения операций умножения комплексных чисел и несложных тождественных преобразований в выражении (7) получим:
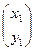 =
= 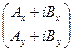 ·
· 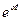 =
= 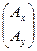 ·
· 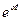 +
+ 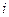
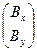 ·
· 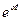 . (8)
. (8)
Аналогично, применяя знак 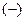 , получаем решение системы (1) с теми же величинами, но только со знаком
, получаем решение системы (1) с теми же величинами, но только со знаком 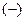 перед мнимой единицей
перед мнимой единицей 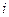 :
:
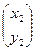 =
= 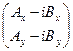 ·
· 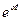 =
= 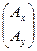 ·
· 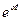 –
– 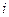
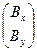 ·
· 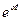 . (9)
. (9)
Известно (была доказана теорема!), что от записей решений системы (1) с использованием выражений (8) и (9) можно перейти к записям:
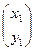 =
= 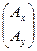 ·
· 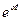 и
и 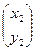 =
= 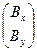 ·
· 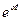 . (10)
. (10)
Учитывая теорему: сумма решений однородной системы уравнений – тоже решение, можем записать общее решение системы уравнений (1):
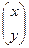 =
=  ·
· 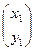 +
+  ·
· 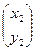 =
=  ·
· 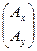 ·
· 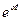 +
+  ·
· 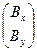 ·
· 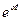 , (11)
, (11)
где  ,
,  - произвольные постоянные. Запись (11) называют общим решением системы уравнений (1) для пары характеристических корней
- произвольные постоянные. Запись (11) называют общим решением системы уравнений (1) для пары характеристических корней 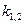 .
.
Если заданы начальные условия: 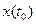 =
= 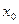 ,
, 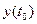 =
= 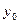 , можно определить такие значения
, можно определить такие значения  ,
,  , что из множества интегральных кривых будет выделена та, которая проходит через точку
, что из множества интегральных кривых будет выделена та, которая проходит через точку 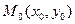 .
.
Случай -3. Корни уравнения ∆(k) = 0 действительные и равные: 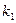 =
= 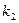 =
= 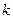 .
.
Для каждого 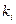 из системы (3) определится набор коэффициентов:
из системы (3) определится набор коэффициентов: 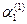 =
= 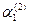 и
и 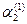 =
= 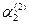 . Это значит, что необходимо как-то учесть равенство (кратность) характеристических корней. В отличие от способа учёта кратных корней при решении уравнений высшего порядка для одной функции, в случае системы уравнений ищут сразу пару решений, используя конструкцию:
. Это значит, что необходимо как-то учесть равенство (кратность) характеристических корней. В отличие от способа учёта кратных корней при решении уравнений высшего порядка для одной функции, в случае системы уравнений ищут сразу пару решений, используя конструкцию: 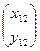 =
= 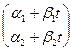 ·
· 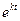 , (12)
, (12)
Так как выражение (12) должно быть решением, то необходимо участвующие параметры подчинить заданной системе уравнений (1). Подставим (12) в систему (1), сократив на число 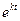 , получим систему тождеств:
, получим систему тождеств:
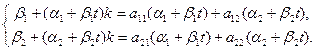 (13)
(13)
Приравнивая в тождествах (13) коэффициенты при одинаковых степенях 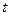 , получаем системы уравнений: при
, получаем системы уравнений: при 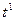 :
: 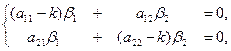 (14)
(14)
при 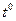 :
: 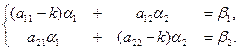 (15)
(15)
Порядок нахождения параметров 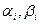 ,
, 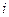 =1,2 из систем уравнений (14) и (15):
=1,2 из систем уравнений (14) и (15):
1). Из системы (14) находим параметры 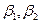 : так как определитель системы равен 0, то ненулевые решения у системы найдутся. Принимая свободную неизвестную
: так как определитель системы равен 0, то ненулевые решения у системы найдутся. Принимая свободную неизвестную 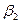 =
=  , получим в выражении (12) участие свободной неизвестной. Параметр
, получим в выражении (12) участие свободной неизвестной. Параметр  будем использовать как произвольную постоянную в записи решения системы (1) – признак общего решения системы!
будем использовать как произвольную постоянную в записи решения системы (1) – признак общего решения системы!
2). Используя найденные параметры 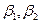 , решаем систему уравнений (15). Это система также имеет ненулевые решения:
, решаем систему уравнений (15). Это система также имеет ненулевые решения: 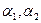 . Принимая свободную неизвестную
. Принимая свободную неизвестную 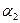 =
=  , получим в выражении (12) участие ещё одной свободной неизвестной. Параметр
, получим в выражении (12) участие ещё одной свободной неизвестной. Параметр  будем использовать как произвольную постоянную в записи решения системы (1) – признак общего решения системы!
будем использовать как произвольную постоянную в записи решения системы (1) – признак общего решения системы!
Итак, получено общее решение системы дифференциальных уравнений (1) для случая кратных действительных корней.
Если заданы начальные условия: 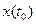 =
= 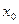 ,
, 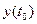 =
= 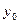 , можно определить такие значения
, можно определить такие значения  ,
,  , что из множества интегральных кривых будет выделена та, которая проходит через точку
, что из множества интегральных кривых будет выделена та, которая проходит через точку 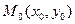 .
.
••• ≡ •••
Пример 1 – 431: Решить систему линейных уравнений: 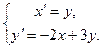
Решение:
1). Найдем характеристические корни системы: 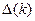 =
= 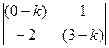 = 0, откуда получаем:
= 0, откуда получаем: 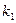 = 1,
= 1, 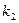 =2. Для каждого
=2. Для каждого 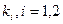 определится набор коэффициентов:
определится набор коэффициентов: 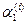 ,
, 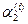 , что определит полный набор решений заданной системы:
, что определит полный набор решений заданной системы:
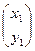 =
= 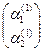 ∙
∙ 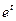 =
= 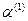 ∙
∙ 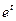 ,
, 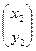 =
= 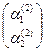 ∙
∙ 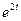 =
= 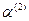 ∙
∙ 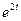 . (1.1)
. (1.1)
2). Для определения векторов 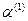 ,
, 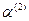 составим систему уравнений:
составим систему уравнений:
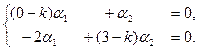 (2.1)
(2.1)
3). Для корня 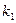 = 1 система (2.1) имеет решение
= 1 система (2.1) имеет решение 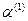 =
= 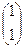 ; для
; для 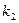 =2 система (2.1) имеет решение:
=2 система (2.1) имеет решение: 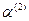 =
= 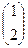 .
.
Замечание: решение системы (2.1) проводится по известным правилам из курса «Линейная алгебра».
4). С учетом полученных векторов 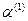 ,
, 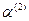 составим общее решение исходной системы дифференциальных уравнений:
составим общее решение исходной системы дифференциальных уравнений:  =1,
=1,  = 0
= 0
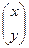 =
= 
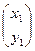 +
+ 
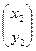 =
= 
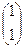 ∙
∙ 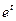 +
+ 
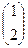 ∙
∙ 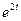 . (3.1)
. (3.1)
Ответ: общее решение системы: 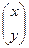 =
= 
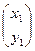 +
+ 
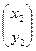 =
= 
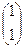 ∙
∙ 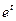 +
+ 
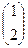 ∙
∙ 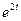 .
.
Пример 2 – 432: Решить систему уравнений: 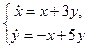 при условии:
при условии: 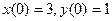 .
.
Решение:
1). Найдем характеристические корни системы: 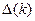 =
= 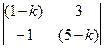 = 0, откуда получаем:
= 0, откуда получаем: 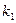 = 2,
= 2, 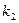 =4. Для каждого
=4. Для каждого 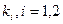 определится набор коэффициентов:
определится набор коэффициентов: 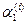 ,
, 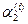 , что определит полный набор решений системы (1):
, что определит полный набор решений системы (1):
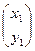 =
= 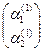 ∙
∙ 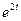 =
= 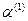 ∙
∙ 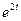 ,
, 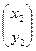 =
= 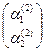 ∙
∙ 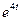 =
= 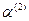 ∙
∙ 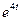 , (1)
, (1)
2). Для определения векторов 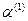 ,
, 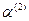 составим систему уравнений:
составим систему уравнений:
 (2)
(2)
3). Для корня 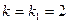 система (2) имеет решение
система (2) имеет решение 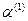 =
= 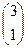 ; для корня
; для корня 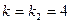 система (2) имеет решение:
система (2) имеет решение: 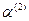 =
= 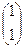 .
.
4). С учетом полученных векторов 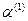 ,
, 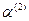 составим общее решение исходной системы дифференциальных уравнений:
составим общее решение исходной системы дифференциальных уравнений: 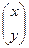 =
= 
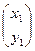 +
+ 
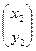 =
= 
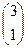 ∙ e 2 t +
∙ e 2 t + 
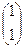 ∙ e 4 t. (3)
∙ e 4 t. (3)
5). Учитывая начальные условия и запись общего решения, получим:
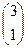 =
= 
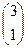 +
+ 
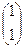 , откуда
, откуда  =1,
=1,  = 0. (4)
= 0. (4)
6). Используя результаты (4), запишем частное решение системы, удовлетворяющее начальным условиям: 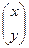 =
= 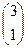 ∙ e 2 t. (5)
∙ e 2 t. (5)
Ответ: Общее решение системы: 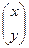 =
= 
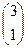 ∙
∙ 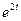 +
+ 
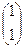 ∙
∙ 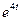 , частное:
, частное: 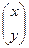 =
= 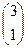 ∙
∙ 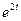 .
.
Пример 3 – 438: Найти частное решение системы: 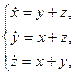 если:
если: 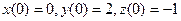 .
.
Решение:
1). Найдем характеристические корни системы: 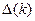 =
= 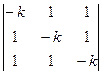 = 0, откуда получаем:
= 0, откуда получаем: 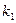 =
= 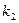 = –1;
= –1; 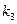 = 2. В этом случае решение системы для кратного корня
= 2. В этом случае решение системы для кратного корня 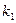 =–1 необходимо искать в виде:
=–1 необходимо искать в виде: 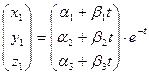 , (1.4)
, (1.4)
2). Подставим (1) исходную систему уравнений:
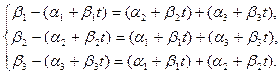 (2.4)
(2.4)
3). Так как в системе уравнений (2.4) каждое уравнение является тождеством, то все неизвестные коэффициенты найдем, приравнивая коэффициенты при одинаковых степенях: 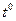 и
и 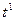 :
:
при 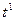 :
: 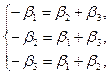 откуда получаем:
откуда получаем: 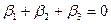 ; (3.4)
; (3.4)
при 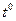 :
: 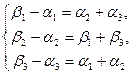 получаем:
получаем: 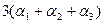 =
= 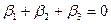 . (4.4)
. (4.4)
В данной задаче, если в уравнении (3.4) принять в качестве свободных неизвестных две из неизвестных 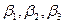 , то из (4.4) получается
, то из (4.4) получается 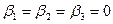 , то есть неизвестные не могут быть свободными в общей системе (3.4),(4.4). Тогда из (4.4):
, то есть неизвестные не могут быть свободными в общей системе (3.4),(4.4). Тогда из (4.4): 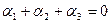 получаем значения остальных параметров:
получаем значения остальных параметров: 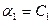 ,
, 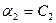 ,
, 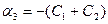 .
.
4). Учитывая полученные в (3) значения коэффициентов, можно представить запись (1) в виде: 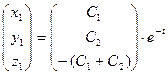 , (5.4)
, (5.4)
5). Для определения вектора 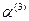 составим систему уравнений:
составим систему уравнений:
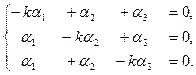 (6.4)
(6.4)
6). Для корня 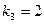 из системы (5) имеем:
из системы (5) имеем: 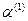 =
= 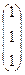 , тогда:
, тогда: 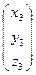 =
= 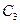 ∙
∙ 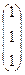 ∙
∙ 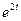 . (7.4)
. (7.4)
7). С учетом полученных решений (4.6) и (6.6), составим общее решение исходной системы дифференциальных уравнений (с учетом свойств матриц):
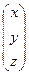 =
= 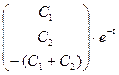 +
+ 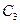 ∙
∙ 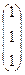 ∙
∙ 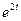 . (8.4)
. (8.4)
8). Учитывая начальные условия и запись общего решения, получим:
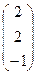 =
= 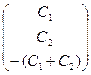 +
+ 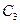 ∙
∙ 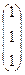 , откуда
, откуда  =1,
=1,  = 1,
= 1, 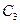 =1. (9.4)
=1. (9.4)
9). Используя результаты (8.6), запишем частное решение системы, удовлетворяющее начальным условиям: 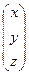 =
= 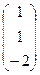 ∙
∙ 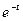 +
+ 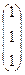 ∙
∙ 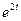 . (10.4)
. (10.4)
Ответ: частное решение системы: 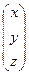 =
= 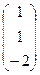 ∙
∙ 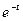 +
+ 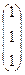 ∙
∙ 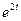 .
.
Пример 4 – 440: Решить систему уравнений: 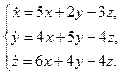
Решение:
1). Найдем характеристические корни системы: 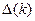 =
= 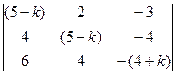 = 0, откуда получаем:
= 0, откуда получаем: 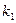 =1,
=1, 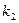 = 2;
= 2; 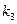 = 3.
= 3.
Замечание: решение уравнения 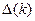 =
= 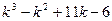 =0 проводится по Виету: угадали все корни как множители числа 6.
=0 проводится по Виету: угадали все корни как множители числа 6.
2). Для каждого 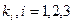 определится набор коэффициентов:
определится набор коэффициентов: 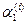 ,
, 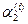 ,
, 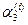 , что определит полный набор решений системы (1):
, что определит полный набор решений системы (1):
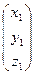 =
= 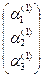 ∙
∙ 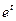 =
= 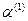 ∙
∙ 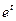 ,
, 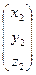 =
= 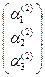 ∙
∙ 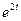 =
= 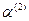 ∙
∙ 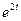 ,
, 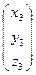 =
= 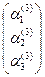 ∙
∙ 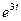 =
= 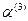 ∙
∙ 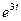 , (1.5)
, (1.5)
3). Для определения векторов 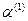 ,
, 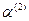 ,
, 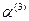 составим систему уравнений:
составим систему уравнений:
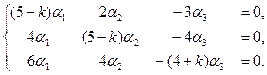 (2.5)
(2.5)
4). Для значения 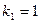 система (2.5) имеет решение:
система (2.5) имеет решение: 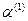 =
= 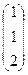 , для значения
, для значения 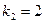 система (2.5) имеет решение:
система (2.5) имеет решение: 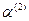 =
= 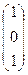 , для значения
, для значения 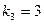 система (2.5) имеет решение:
система (2.5) имеет решение: 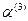 =
= 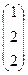 .
.
5). С учетом полученных векторов 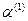 ,
,
 2015-05-12
2015-05-12 3865
3865