Угол между векторами на плоскости и в пространстве.
Пусть на плоскости или в трехмерном пространстве заданы два ненулевых вектора 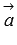 и
и 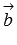 . Отложим от произвольной точки O векторы
. Отложим от произвольной точки O векторы 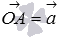 и
и 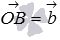 . Тогда справедливо следующее определение.
. Тогда справедливо следующее определение.
Определение.
Углом между векторами 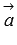 и
и 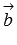 называется угол между лучами OA и OB.
называется угол между лучами OA и OB.
Угол между векторами 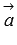 и
и 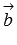 будем обозначать как
будем обозначать как 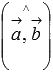 .
.
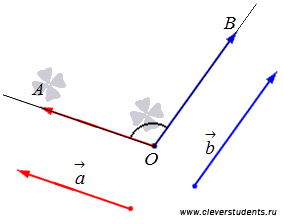
Угол между векторами может принимать значения от 0 до 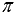 или, что то же самое, от
или, что то же самое, от 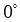 до
до 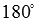 .
.
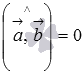 когда векторы
когда векторы  и
и  сонаправленные,
сонаправленные, 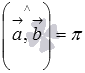 когда векторы
когда векторы 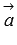 и
и 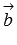 противоположно направленные.
противоположно направленные.
Определение.
Векторы 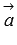 и
и 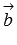 называются перпендикулярными, если угол между ними равен
называются перпендикулярными, если угол между ними равен 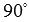 (
(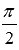 радиан).
радиан).
Если хотя бы один из векторов 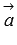 и
и 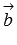 нулевой, то угол
нулевой, то угол 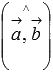 не определен.
не определен.
Нахождение угла между векторами, примеры и решения.
Косинус угла между векторами 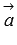 и
и 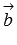 , а значит и сам угол, в общем случае может быть найден либо с использованием скалярного произведения векторов, либо с использованием теоремы косинусов для треугольника, построенного на векторах
, а значит и сам угол, в общем случае может быть найден либо с использованием скалярного произведения векторов, либо с использованием теоремы косинусов для треугольника, построенного на векторах 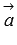 и
и 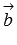 .
.
Разберем эти случаи.
По определению скалярное произведение векторов есть 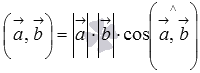 . Если векторы
. Если векторы  и
и 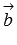 ненулевые, то можно разделить обе части последнего равенства на произведение длин векторов
ненулевые, то можно разделить обе части последнего равенства на произведение длин векторов 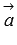 и
и 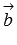 , и мы получим формулу для нахождения косинуса угла между ненулевыми векторами:
, и мы получим формулу для нахождения косинуса угла между ненулевыми векторами: 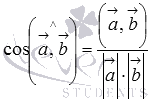 . Эту формулу можно использовать, если известны длины векторов и их скалярное произведение.
. Эту формулу можно использовать, если известны длины векторов и их скалярное произведение.
Пример.
Вычислите косинус угла между векторами 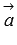 и
и 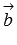 , а также найдите сам угол, если длины векторов
, а также найдите сам угол, если длины векторов 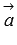 и
и 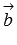 равны 3 и 6 соответственно, а их скалярное произведение равно -9.
равны 3 и 6 соответственно, а их скалярное произведение равно -9.
Решение.
В условии задачи даны все величины необходимые для применения формулы 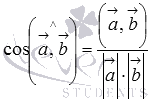 . Вычисляем косинус угла между векторами
. Вычисляем косинус угла между векторами  и
и  :
: 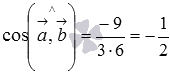 .
.
Теперь находим угол между векторами: 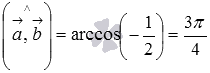 .
.
Ответ:
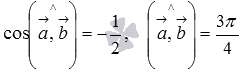 .
.
Существуют задачи, где векторы заданы координатами в прямоугольной системе координат на плоскости или в пространстве. В этих случаях для нахождения косинуса угла между векторами можно использовать все ту же формулу 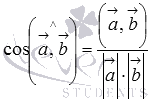 , но в координатной форме. Получим ее.
, но в координатной форме. Получим ее.
Длина вектора есть корень квадратный из суммы квадратов его координат, скалярное произведение векторов равно сумме произведений соответствующих координат. Следовательно, формула для вычисления косинуса угла между векторами  на плоскости имеет вид
на плоскости имеет вид 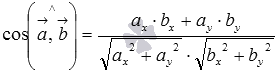 , а для векторов
, а для векторов  в трехмерном пространстве -
в трехмерном пространстве - 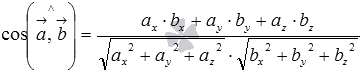 .
.
Пример.
Найдите угол между векторами 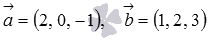 , заданными в прямоугольной системе координат.
, заданными в прямоугольной системе координат.
Решение.
Можно сразу воспользоваться формулой 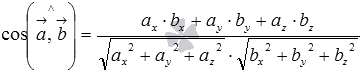 :
:
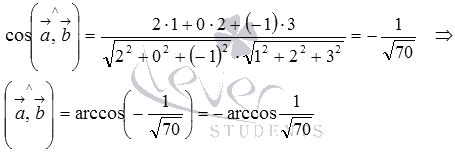
А можно для нахождения косинуса угла между векторами использовать формулу 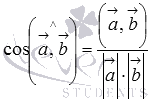 , предварительно вычислив длины векторов и скалярное произведение по координатам:
, предварительно вычислив длины векторов и скалярное произведение по координатам:
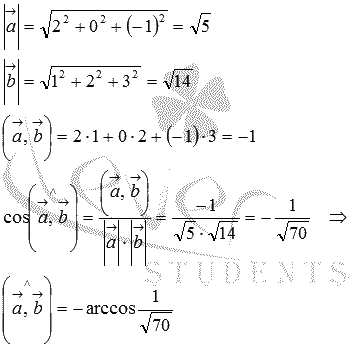
Ответ:
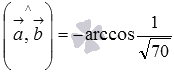 .
.
К предыдущему случаю сводится задача, когда даны координаты трех точек (например А, В и С) в прямоугольной системе координат и требуется найти какой-нибудь угол (например, 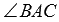 ).
).
Действительно, угол 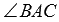 равен углу между векторами
равен углу между векторами 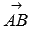 и
и 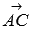 . Координаты этих векторов вычисляются как разность соответствующих координат точек конца и начала вектора.
. Координаты этих векторов вычисляются как разность соответствующих координат точек конца и начала вектора.
Пример.
На плоскости в декартовой системе координат заданы координаты трех точек 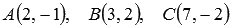 . Найдите косинус угла между векторами
. Найдите косинус угла между векторами 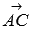 и
и 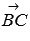 .
.
Решение.
Определим координаты векторов 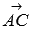 и
и 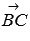 по координатам заданных точек:
по координатам заданных точек:
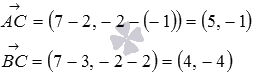
Теперь воспользуемся формулой для нахождения косинуса угла между векторами на плоскости в координатах:
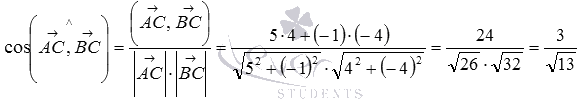
Ответ:
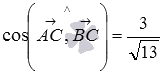 .
.
Угол между векторами 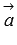 и
и 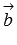 также можно вычислить по теореме косинусов. Если отложить от точки O векторы
также можно вычислить по теореме косинусов. Если отложить от точки O векторы 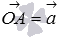 и
и 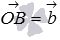 , то по теореме косинусов в треугольнике ОАВ мы можем записать
, то по теореме косинусов в треугольнике ОАВ мы можем записать 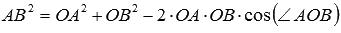 , что эквивалентно равенству
, что эквивалентно равенству 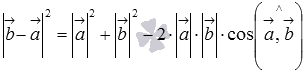 , откуда находим косинус угла между векторами
, откуда находим косинус угла между векторами 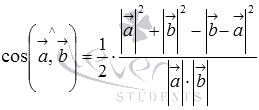 . Для применения полученной формулы нам нужны лишь длины векторов
. Для применения полученной формулы нам нужны лишь длины векторов 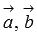 и
и 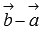 , которые легко находятся по координатам векторов
, которые легко находятся по координатам векторов 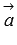 и
и 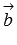 . Однако, этот метод практически не используется, так как косинус угла между векторами проще найти по формуле
. Однако, этот метод практически не используется, так как косинус угла между векторами проще найти по формуле 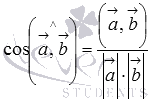 .
.
Вычисление ортогональной проекции(сво-во проекции):
Проекция вектора 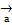 на ось l равна произведению модуля вектора
на ось l равна произведению модуля вектора 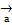 на косинус угла φ между вектором и осью, т.е. пр
на косинус угла φ между вектором и осью, т.е. пр 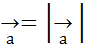 cosφ.
cosφ.
Док-во: Если φ= 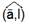 <
<  , то прl
, то прl 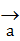 =+
=+ 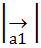 =
= 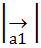 *cos φ.
*cos φ.
Если φ>  (φ≤
(φ≤ 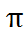 ), то прl
), то прl 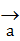 =-
=- 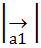 =-
=- 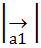 * cos(
* cos(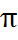 –φ) =
–φ) = 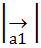 cosφ (см.рис10)
cosφ (см.рис10)
Если φ=  , то прl
, то прl 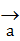 = 0 =
= 0 = 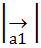 соs φ.
соs φ.
Следствие: Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нуле, если этот угол – прямой.
Следствие: Проекции равных векторов на одну и ту же ось равны между собой.
Вычисление ортогональной проекции суммы векторов (сво-во проекции):
Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.
Док-во: Пусть, например, 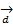 =
= 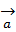 +
+ 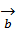 +
+ 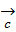 . Имеем прl
. Имеем прl 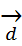 =+
=+ 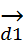 =+
=+ 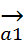 +
+ 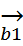 -
- 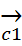 , т.е. прl(
, т.е. прl(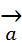 +
+ 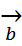 +
+ 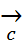 ) = прl
) = прl 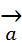 + прl
+ прl  + прl
+ прl  (см.рис11)
(см.рис11)
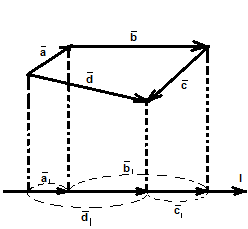
РИС. 11
Вычисление произведения вектора на число:
При умножеии вектора 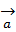 на число λ его проекция на ось так же умножается на это число, т.е. прl (λ*
на число λ его проекция на ось так же умножается на это число, т.е. прl (λ* 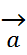 )= λ* прl
)= λ* прl 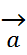 .
.
Док-во: При λ > 0 имеем прl (λ* 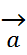 )=
)= 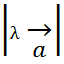 *cos φ = λ*
*cos φ = λ* 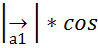 φ = λ*прl
φ = λ*прl 
При λl (λ*  )=
)= 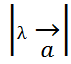 *cos(
*cos(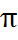 –φ)=-
–φ)=- 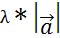 * (-cosφ) =
* (-cosφ) = 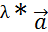 * cosφ= λ *прl
* cosφ= λ *прl 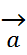 .
.
Свойство справедливо и при 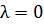
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
 2015-05-13
2015-05-13 20312
20312