Кроме декартовой системы координат для определения положения точек на плоскости часто используют полярную систему координат.
| rrr |
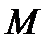 это
это
упорядоченная пара чисел 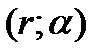 .
. 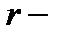 это расстояние от
это расстояние от
| r |
| М |
 (называемой полюсом) до
(называемой полюсом) до
| ∝ |
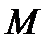 .
. 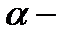 угол(выраженный в радианах) между
угол(выраженный в радианах) между
| О |
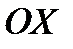 и отрезком
и отрезком 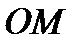 рис.15.
рис.15.
рис.15
Если на плоскости введены одновременно две системы координат декартова система и полярная система, то между ними существует связь (рис.16).
| ∝ |
| А |
| В |
| r |
| X |
| Y |
Рис.16
Из 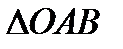 (рис.16.) следуют формулы связи
(рис.16.) следуют формулы связи
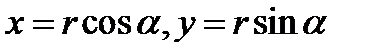 ,
, 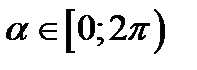 (2.23)
(2.23)
И наоборот
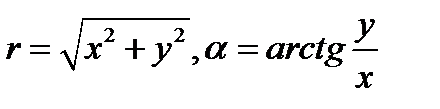
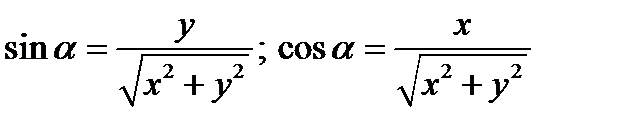 (2.24)
(2.24)
Пример 2.9. Изобразить точку 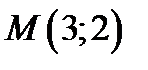 на координатной плоскости.
на координатной плоскости.
Решение. Сначала нужно поинтересоваться, в каких координатах задана данная точка.
Если в декартовых координатах, то рисунок будет таким (рис.17), если в полярных, то таким (рис.18)
| М |
| М |
| r=3 |
| 115° |
Рис.17 рис.18
Действительно 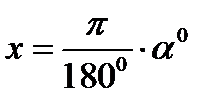 .Следовательно
.Следовательно 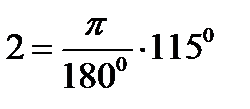 (см. формулу 2.21).
(см. формулу 2.21).
Упражнение. Изобразить точки заданные в полярной системе координат
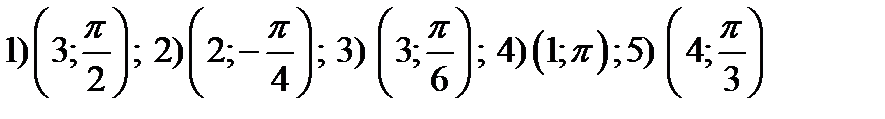
и найти прямоугольные координаты этих точек.
Упражнение. Изобразить точки заданные в декартовой системе координат:
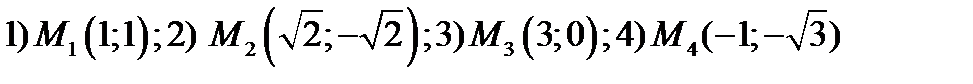
и найти полярные координаты этих точек.
Если полярный радиус 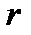 и полярный угол
и полярный угол 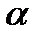 связаны друг с другом формулой
связаны друг с другом формулой 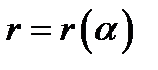 ,
,
то при изменении угла 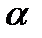 будет изменяться и полярный радиус. Точки
будет изменяться и полярный радиус. Точки 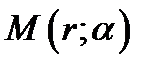 при непрерывном изменении угла
при непрерывном изменении угла 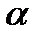 опишут некоторую кривую.
опишут некоторую кривую.
Пример 2.10. Построим кривые: 1) 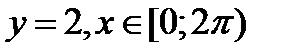 в декартовой системе координат;
в декартовой системе координат;
2) 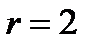
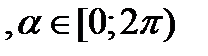 в полярной системе координат.
в полярной системе координат.
Соответствующие эскизы этих кривых приведены ниже
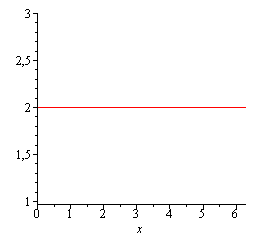
Пример 2.11. Построить по точкам кривые: 1) 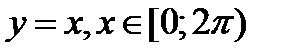 в декартовой системе координат;
в декартовой системе координат;
2) 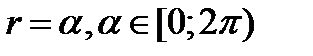 в полярной системе координат.
в полярной системе координат.
Соответствующие эскизы этих кривых приведены ниже
Контрольные вопросы.
I. Дайте определения кривых второго порядка:
1) параболы, 2) эллипса, 3)гиперболы
II. На какой оси координат лежат фокусы (с) данных кривых
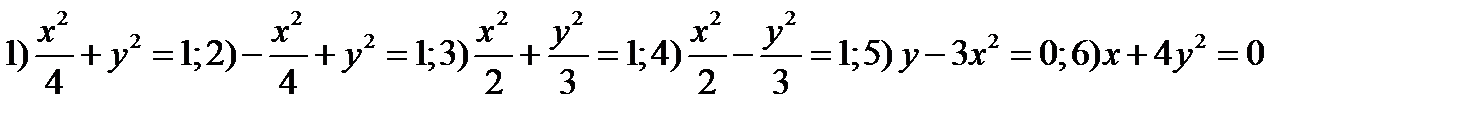
III. Напишите формулы перехода от декартовой системы координат к полярной
системе и наоборот.
IV. Пусть 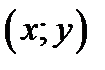
 произвольная точка в декартовой системе координат, а
произвольная точка в декартовой системе координат, а 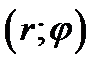
произвольная точка в полярной системе координат. Дайте рисунки линий
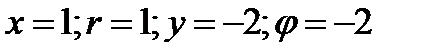 .
.
 2015-05-13
2015-05-13 486
486








