ПУСТЬ ТОЧКА
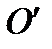
В СИСТЕМЕ КООРДИНАТ
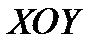
ИМЕЕТ КООРДИНАТЫ
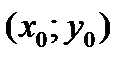
. ПОМЕСТИМ НАЧАЛО НОВОЙ СИСТЕМЫ КООРДИНАТ
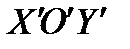
В ТОЧКУ
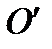
. ОСЬ
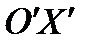
НАПРАВИМ ПАРАЛЛЕЛЬНО ОСИ
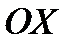
, А ОСЬ
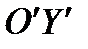
ПАРАЛЛЕЛЬНО ОСИ
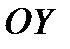
. ТОГДА В НОВОЙ СИСТЕМЕ КООРДИНАТ
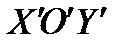
ТОЧКА
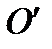
БУДЕТ ИМЕТЬ КООРДИНАТЫ
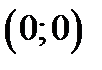
(РИС.13). ЕСЛИ ТЕПЕРЬ НА ПЛОСКОСТИ РАССМОТРИМ ПРОИЗВОЛЬНУЮ ТОЧКУ
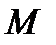
, ИМЕЮЩУЮ В СТАРОЙ СИСТЕМЕ КООРДИНАТ
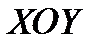
КООРДИНАТЫ
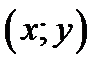
, ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ ТОЧКА БУДЕТ ИМЕТЬ КООРДИНАТЫ
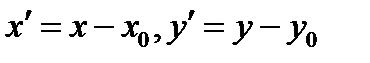
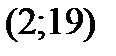
ПЕРЕХОД ОТ КООРДИНАТНОЙ СИСТЕМЫ 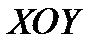 К СИСТЕМЕ
К СИСТЕМЕ 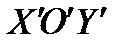 НАЗОВЕМ ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ КООРДИНАТ (РИС.13).
НАЗОВЕМ ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ КООРДИНАТ (РИС.13).
РИС.13
ПРИМЕР 2.5. НА РИС.14 ПРИВЕДЁН ЧЕРТЁЖ ПАРАБОЛЫ И ВЫПИСАНЫ ЕЁ УРАВНЕНИЯ В СТАРОЙ И НОВОЙ СИСТЕМАХ ДЕКАРТОВЫХ КООРДИНАТ. НОВАЯ СИСТЕМА ПОЛУЧЕНА ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ СТАРОЙ СИСТЕМЫ.

1
РИС.14
В СТАРОЙ СИСТЕМЕ КООРДИНАТ 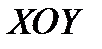 УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД
УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД
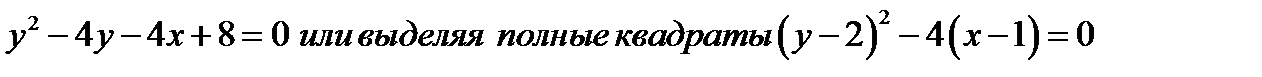
В НОВОЙ «КАНОНИЧЕСКОЙ» СИСТЕМЕ КООРДИНАТ 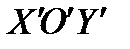 УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД
УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД
(СМ. ФОРМУЛУ (2.19))
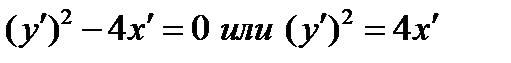 . ЛИНИЯ ПАРАБОЛА.
. ЛИНИЯ ПАРАБОЛА.
ЗАМЕЧАНИЕ. ПРИВЕДЁМ ПРИМЕР ЧЕРТЕЖА ПАРАБОЛЫ, У КОТОРОЙ УРАВНЕНИЕ НЕ КАНОНИЧЕСКОЕ. В ДАННОМ СЛУЧАЕ ДЛЯ ПОЛУЧЕНИЯ «КАНОНИЧЕСКОЙ» СИСТЕМЫ КООРДИНАТ 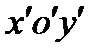 ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ
ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ 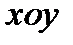 .
.

В ДЕКАРТОВОЙ ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ
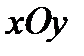
, КОТОРАЯ НЕ ЯВЛЯЕТСЯ «КАНОНИЧЕСКОЙ», УРАВНЕНИЕ ПАРАБОЛЫ В ОБЩЕМ СЛУЧАЕ ИМЕЕТ ВИД:
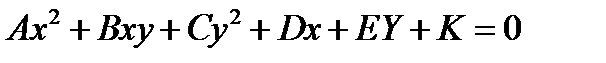
. КРИВАЯ ПАРАБОЛЫ НЕ СИММЕТРИЧНА НИ ОДНОЙ ИЗ КООРДИНАТНЫХ ОСЕЙ. ЕСЛИ ПАРАЛЛЕЛЬНЫМ СДВИГОМ СИСТЕМЫ КООРДИНАТ НАЧАЛО КООРДИНАТ

ПЕРЕМЕСТИТЬ В ВЕРШИНУ ПАРАБОЛЫ В ТОЧКУ
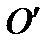
, А ЗАТЕМ ОСИ ПОВЕРНУТЬ СОГЛАСНО РИСУНКУ, ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ
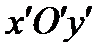
УРАВНЕНИЕ ПАРАБОЛЫ СТАНОВИТСЯ КАНОНИЧЕСКИМ (РИС15)
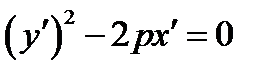
РИС.15
ПРИМЕР 2.6 НА РИС.16 ПРИВЕДЁН ЧЕРТЁЖ ЭЛЛИПСА И ВЫПИСАНЫ ЕГО УРАВНЕНИЯ В СТАРОЙ И НОВОЙ СИСТЕМАХ ДЕКАРТОВЫХ КООРДИНАТ. НОВАЯ СИСТЕМА ПОЛУЧЕНА ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ СТАРОЙ СИСТЕМЫ.

РИС.16
В СТАРОЙ СИСТЕМЕ КООРДИНАТ 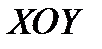 УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД
УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД
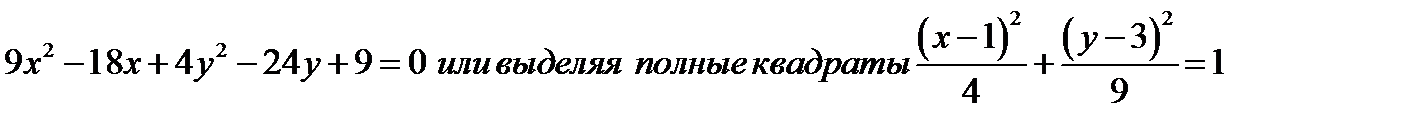
В НОВОЙ «КАНОНИЧЕСКОЙ» СИСТЕМЕ КООРДИНАТ 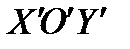 УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД
УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД
(СМ. ФОРМУЛУ (2.19)) 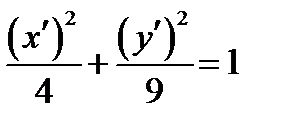 . ЛИНИЯ ЭЛЛИПС.
. ЛИНИЯ ЭЛЛИПС.
ЗАМЕЧАНИЕ. ПРИВЕДЁМ ПРИМЕР ЧЕРТЕЖА ЭЛЛИПСА, У КОТОРОГО УРАВНЕНИЕ НЕ КАНОНИЧЕСКОЕ. В ДАННОМ СЛУЧАЕ ДЛЯ ПОЛУЧЕНИЯ «КАНОНИЧЕСКОЙ» СИСТЕМЫ КООРДИНАТ
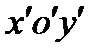
ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ
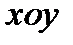
.

В ДЕКАРТОВОЙ ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ
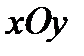
, КОТОРАЯ НЕ ЯВЛЯЕТСЯ «КАНОНИЧЕСКОЙ», УРАВНЕНИЕ ЭЛЛИПСА ОБЫЧНО ИМЕЕТ ВИД:
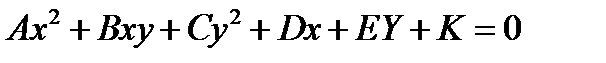
КРИВАЯ ЭЛЛИПСА НЕ СИММЕТРИЧНА ОТНОСИТЕЛЬНО КООРДИНАТНЫХ ОСЕЙ. ЕСЛИ НАЧАЛО КООРДИНАТ

ПЕРЕМЕСТИТЬ В ЦЕНТР СИММЕТРИИ ЭЛЛИПСА ТОЧКУ
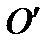
, А ОСИ ПОВЕРНУТЬ СОГЛАСНО РИСУНКУ, ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ЭЛЛИПСА СТАНОВИТСЯ КАНОНИЧЕСКИМ (РИС.17)
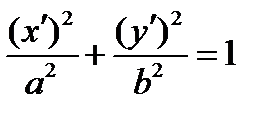
РИС.17
ПРИМЕР 2.7. НА РИС.18 ПРИВЕДЁН ЧЕРТЁЖ ГИПЕРБОЛЫ И ВЫПИСАНЫ ЕЁ УРАВНЕНИЯ В СТАРОЙ 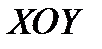 И НОВОЙ
И НОВОЙ 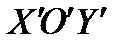 СИСТЕМАХ ДЕКАРТОВЫХ КООРДИНАТ. НОВАЯ СИСТЕМА ПОЛУЧЕНА ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ СТАРОЙ СИСТЕМЫ.
СИСТЕМАХ ДЕКАРТОВЫХ КООРДИНАТ. НОВАЯ СИСТЕМА ПОЛУЧЕНА ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ СТАРОЙ СИСТЕМЫ.

РИС.17
В СТАРОЙ СИСТЕМЕ КООРДИНАТ 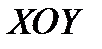 УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД
УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД


В НОВОЙ «КАНОНИЧЕСКОЙ» СИСТЕМЕ КООРДИНАТ 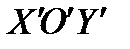 УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД
УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД
(СМ. ФОРМУЛУ (2.19))
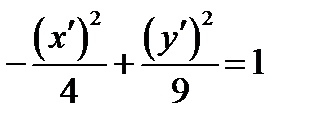 . ЛИНИЯ ГИПЕРБОЛА.
. ЛИНИЯ ГИПЕРБОЛА.
ЗАМЕЧАНИЕ. ПРИВЕДЁМ ПРИМЕР ЧЕРТЕЖА ГИПЕРБОЛЫ, У КОТОРОЙ УРАВНЕНИЕ НЕ КАНОНИЧЕСКОЕ. В ДАННОМ СЛУЧАЕ ДЛЯ ПОЛУЧЕНИЯ КАНОНИЧЕСКОЙ СИСТЕМЫ КООРДИНАТ 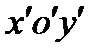 ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ
ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ 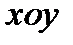 .
.

В ДЕКАРТОВОЙ ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ
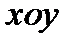
, КОТОРАЯ НЕ ЯВЛЯЕТСЯ «КАНОНИЧЕСКОЙ», КРИВАЯ ВЫГЛЯДИТ ТАК. ЕСЛИ НАЧАЛО КООРДИНАТ

ПЕРЕМЕСТИТЬ ПАРАЛЛЕЛЬНЫМ СДВИГОМ В ЦЕНТР СИММЕТРИИ ГИПЕРБОЛЫ В ТОЧКУ
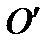
, А ЗАТЕМ ОСИ
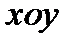
ПОВЕРНУТЬ СОГЛАСНО РИСУНКУ, ТО В НОВОЙ «КАНОНИЧЕСКОЙ» СИСТЕМЕ КООРДИНАТ
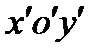 УРАВНЕНИЕ ГИПЕРБОЛЫ
УРАВНЕНИЕ ГИПЕРБОЛЫ СТАНОВИТСЯ КАНОНИЧЕСКИМ (РИС.18)
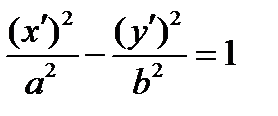
РИС.18
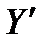
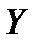
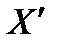
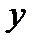
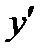
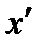

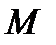
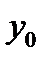
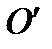
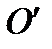 В СИСТЕМЕ КООРДИНАТ
В СИСТЕМЕ КООРДИНАТ 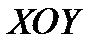 ИМЕЕТ КООРДИНАТЫ
ИМЕЕТ КООРДИНАТЫ 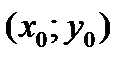 . ПОМЕСТИМ НАЧАЛО НОВОЙ СИСТЕМЫ КООРДИНАТ
. ПОМЕСТИМ НАЧАЛО НОВОЙ СИСТЕМЫ КООРДИНАТ 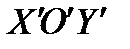 В ТОЧКУ
В ТОЧКУ 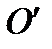 . ОСЬ
. ОСЬ 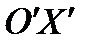 НАПРАВИМ ПАРАЛЛЕЛЬНО ОСИ
НАПРАВИМ ПАРАЛЛЕЛЬНО ОСИ 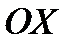 , А ОСЬ
, А ОСЬ 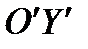 ПАРАЛЛЕЛЬНО ОСИ
ПАРАЛЛЕЛЬНО ОСИ 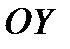 . ТОГДА В НОВОЙ СИСТЕМЕ КООРДИНАТ
. ТОГДА В НОВОЙ СИСТЕМЕ КООРДИНАТ 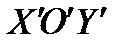 ТОЧКА
ТОЧКА 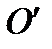 БУДЕТ ИМЕТЬ КООРДИНАТЫ
БУДЕТ ИМЕТЬ КООРДИНАТЫ 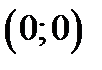 (РИС.13). ЕСЛИ ТЕПЕРЬ НА ПЛОСКОСТИ РАССМОТРИМ ПРОИЗВОЛЬНУЮ ТОЧКУ
(РИС.13). ЕСЛИ ТЕПЕРЬ НА ПЛОСКОСТИ РАССМОТРИМ ПРОИЗВОЛЬНУЮ ТОЧКУ 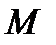 , ИМЕЮЩУЮ В СТАРОЙ СИСТЕМЕ КООРДИНАТ
, ИМЕЮЩУЮ В СТАРОЙ СИСТЕМЕ КООРДИНАТ 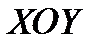 КООРДИНАТЫ
КООРДИНАТЫ 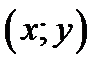 , ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ ТОЧКА БУДЕТ ИМЕТЬ КООРДИНАТЫ
, ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ ТОЧКА БУДЕТ ИМЕТЬ КООРДИНАТЫ 
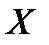
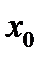
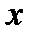
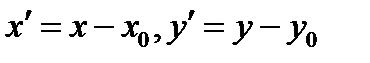
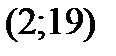
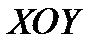 К СИСТЕМЕ
К СИСТЕМЕ 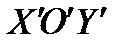 НАЗОВЕМ ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ КООРДИНАТ (РИС.13).
НАЗОВЕМ ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ КООРДИНАТ (РИС.13).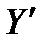

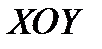 УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД
УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД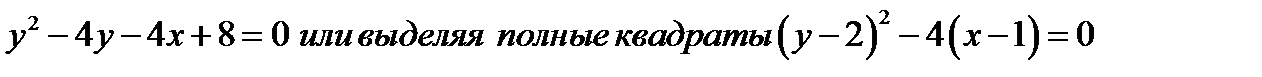
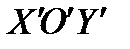 УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД
УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД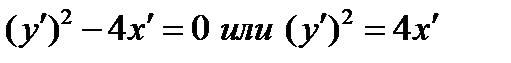 . ЛИНИЯ ПАРАБОЛА.
. ЛИНИЯ ПАРАБОЛА.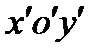 ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ
ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ 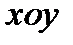 .
.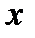

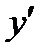
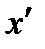
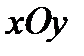 , КОТОРАЯ НЕ ЯВЛЯЕТСЯ «КАНОНИЧЕСКОЙ», УРАВНЕНИЕ ПАРАБОЛЫ В ОБЩЕМ СЛУЧАЕ ИМЕЕТ ВИД:
, КОТОРАЯ НЕ ЯВЛЯЕТСЯ «КАНОНИЧЕСКОЙ», УРАВНЕНИЕ ПАРАБОЛЫ В ОБЩЕМ СЛУЧАЕ ИМЕЕТ ВИД: 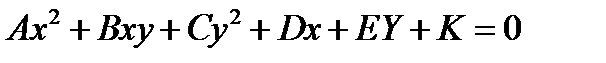 . КРИВАЯ ПАРАБОЛЫ НЕ СИММЕТРИЧНА НИ ОДНОЙ ИЗ КООРДИНАТНЫХ ОСЕЙ. ЕСЛИ ПАРАЛЛЕЛЬНЫМ СДВИГОМ СИСТЕМЫ КООРДИНАТ НАЧАЛО КООРДИНАТ
. КРИВАЯ ПАРАБОЛЫ НЕ СИММЕТРИЧНА НИ ОДНОЙ ИЗ КООРДИНАТНЫХ ОСЕЙ. ЕСЛИ ПАРАЛЛЕЛЬНЫМ СДВИГОМ СИСТЕМЫ КООРДИНАТ НАЧАЛО КООРДИНАТ  ПЕРЕМЕСТИТЬ В ВЕРШИНУ ПАРАБОЛЫ В ТОЧКУ
ПЕРЕМЕСТИТЬ В ВЕРШИНУ ПАРАБОЛЫ В ТОЧКУ 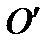 , А ЗАТЕМ ОСИ ПОВЕРНУТЬ СОГЛАСНО РИСУНКУ, ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ
, А ЗАТЕМ ОСИ ПОВЕРНУТЬ СОГЛАСНО РИСУНКУ, ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ 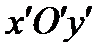 УРАВНЕНИЕ ПАРАБОЛЫ СТАНОВИТСЯ КАНОНИЧЕСКИМ (РИС15)
УРАВНЕНИЕ ПАРАБОЛЫ СТАНОВИТСЯ КАНОНИЧЕСКИМ (РИС15) 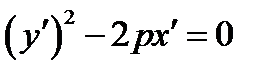
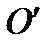
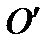

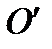
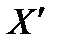
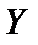
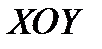 УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД
УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД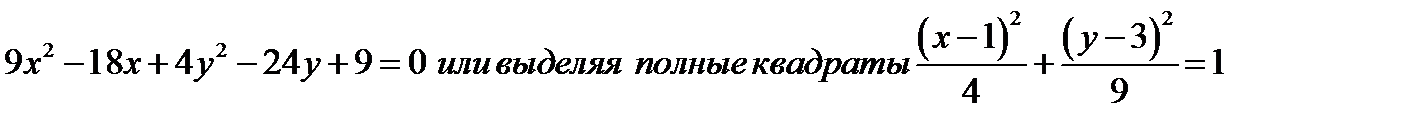
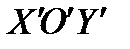 УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД
УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД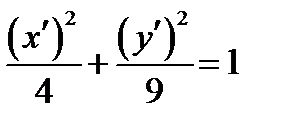 . ЛИНИЯ ЭЛЛИПС.
. ЛИНИЯ ЭЛЛИПС.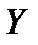
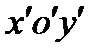 ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ
ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ 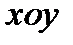 .
. 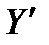
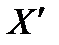

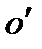
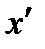
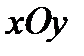 , КОТОРАЯ НЕ ЯВЛЯЕТСЯ «КАНОНИЧЕСКОЙ», УРАВНЕНИЕ ЭЛЛИПСА ОБЫЧНО ИМЕЕТ ВИД:
, КОТОРАЯ НЕ ЯВЛЯЕТСЯ «КАНОНИЧЕСКОЙ», УРАВНЕНИЕ ЭЛЛИПСА ОБЫЧНО ИМЕЕТ ВИД: 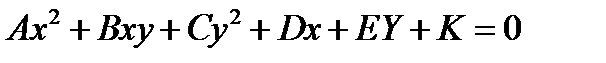 КРИВАЯ ЭЛЛИПСА НЕ СИММЕТРИЧНА ОТНОСИТЕЛЬНО КООРДИНАТНЫХ ОСЕЙ. ЕСЛИ НАЧАЛО КООРДИНАТ
КРИВАЯ ЭЛЛИПСА НЕ СИММЕТРИЧНА ОТНОСИТЕЛЬНО КООРДИНАТНЫХ ОСЕЙ. ЕСЛИ НАЧАЛО КООРДИНАТ  ПЕРЕМЕСТИТЬ В ЦЕНТР СИММЕТРИИ ЭЛЛИПСА ТОЧКУ
ПЕРЕМЕСТИТЬ В ЦЕНТР СИММЕТРИИ ЭЛЛИПСА ТОЧКУ 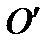 , А ОСИ ПОВЕРНУТЬ СОГЛАСНО РИСУНКУ, ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ЭЛЛИПСА СТАНОВИТСЯ КАНОНИЧЕСКИМ (РИС.17)
, А ОСИ ПОВЕРНУТЬ СОГЛАСНО РИСУНКУ, ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ЭЛЛИПСА СТАНОВИТСЯ КАНОНИЧЕСКИМ (РИС.17) 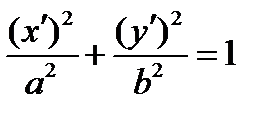
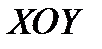 И НОВОЙ
И НОВОЙ 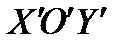 СИСТЕМАХ ДЕКАРТОВЫХ КООРДИНАТ. НОВАЯ СИСТЕМА ПОЛУЧЕНА ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ СТАРОЙ СИСТЕМЫ.
СИСТЕМАХ ДЕКАРТОВЫХ КООРДИНАТ. НОВАЯ СИСТЕМА ПОЛУЧЕНА ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ СТАРОЙ СИСТЕМЫ.

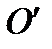
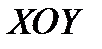 УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД
УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД

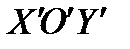 УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД
УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД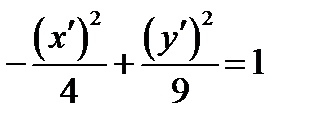 . ЛИНИЯ ГИПЕРБОЛА.
. ЛИНИЯ ГИПЕРБОЛА.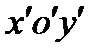 ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ
ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ 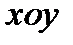 .
.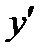
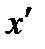
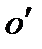
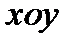 , КОТОРАЯ НЕ ЯВЛЯЕТСЯ «КАНОНИЧЕСКОЙ», КРИВАЯ ВЫГЛЯДИТ ТАК. ЕСЛИ НАЧАЛО КООРДИНАТ
, КОТОРАЯ НЕ ЯВЛЯЕТСЯ «КАНОНИЧЕСКОЙ», КРИВАЯ ВЫГЛЯДИТ ТАК. ЕСЛИ НАЧАЛО КООРДИНАТ  ПЕРЕМЕСТИТЬ ПАРАЛЛЕЛЬНЫМ СДВИГОМ В ЦЕНТР СИММЕТРИИ ГИПЕРБОЛЫ В ТОЧКУ
ПЕРЕМЕСТИТЬ ПАРАЛЛЕЛЬНЫМ СДВИГОМ В ЦЕНТР СИММЕТРИИ ГИПЕРБОЛЫ В ТОЧКУ 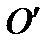 , А ЗАТЕМ ОСИ
, А ЗАТЕМ ОСИ 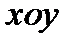 ПОВЕРНУТЬ СОГЛАСНО РИСУНКУ, ТО В НОВОЙ «КАНОНИЧЕСКОЙ» СИСТЕМЕ КООРДИНАТ
ПОВЕРНУТЬ СОГЛАСНО РИСУНКУ, ТО В НОВОЙ «КАНОНИЧЕСКОЙ» СИСТЕМЕ КООРДИНАТ 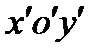 УРАВНЕНИЕ ГИПЕРБОЛЫ СТАНОВИТСЯ КАНОНИЧЕСКИМ (РИС.18)
УРАВНЕНИЕ ГИПЕРБОЛЫ СТАНОВИТСЯ КАНОНИЧЕСКИМ (РИС.18) 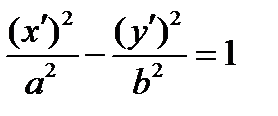
 2015-05-13
2015-05-13 751
751








