Теория:
Функцию, заданную формулой y = logax, называют логарифмической функцией с основанием a.
(a >0, a ≠1)
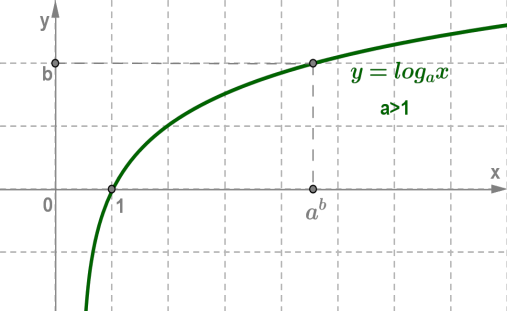
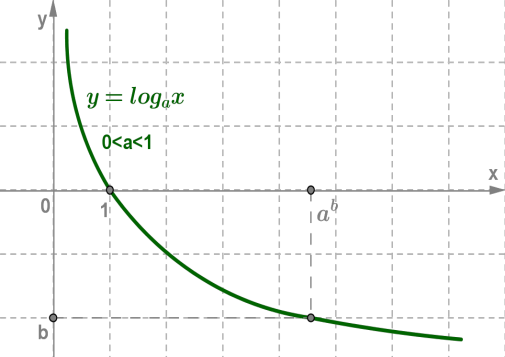
Основные свойства логарифмической функции:
1. Область определения логарифмической функции - множество всех положительных чисел.
D (f)=(0;+∞);
2. Множество значений логарифмической функции - множество R всех действительных чисел.
E (f)=(−∞;+∞);
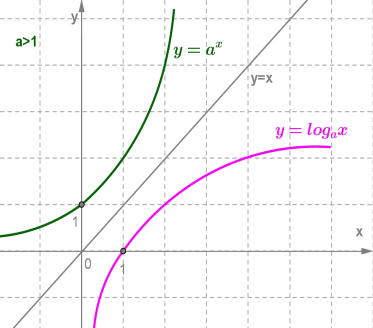
3. Логарифмическая функция на всей области определения возрастает при a >1 или убывает
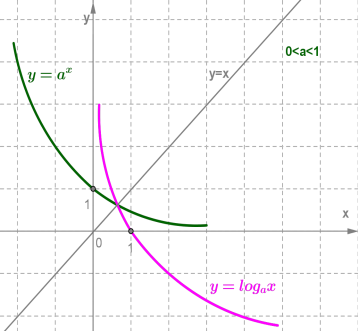
при 0< a <1.
Обрати внимание!
Логарифмическая функция не является ни четной, ни нечетной;
не имеет ни наибольшего, ни наименьшего значений;
не ограничена сверху, не ограничена снизу;
График любой логарифмической функции y = logax проходит через точку (1;0).
Построим графики двух функций
Пример:
1. y = log 2 x, основание 2>1
| x | ||||||
| y = log 2 x | −2 | −1 |
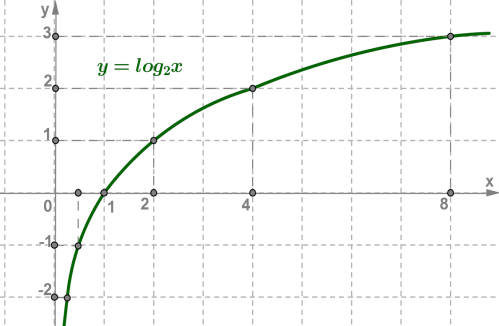
Пример:
2. y = log 13 x основание 0<13<1
| x | |||||
| y = log 13 x | −2 | −1 |
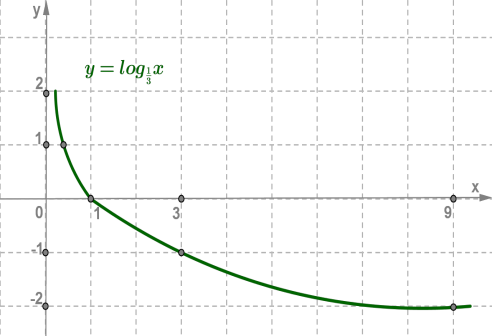
Логарифмическая функция y = logax и показательная функция y = ax, где (a >0, a ≠1), взаимно обратны.
Тригонометрическая функция, ее свойства и график, аналогичные преобразования (y=sin x; y=cos x; y=tg x)
Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла (дуги) в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.
К тригонометрическим функциям относятся:
прямые тригонометрические функции
- синус (
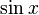 )
) - косинус (
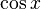 )
)
производные тригонометрические функции
- тангенс (
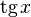 )
) - котангенс (
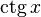 )
)
другие тригонометрические функции
- секанс (
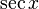 )
) - косеканс (
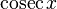 )
)
В западной литературе тангенс, котангенс и косеканс обозначаются 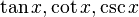 .
.
Кроме этих шести, существуют также некоторые редко используемые тригонометрические функции (версинус и т.д.), а также обратные тригонометрические функции (арксинус, арккосинус и т. д.), рассматриваемые в отдельных статьях.
Синус и косинус вещественного аргумента представляют собой периодические, непрерывные и бесконечно дифференцируемые вещественнозначные функции. Остальные четыре функции на вещественной оси также вещественнозначные, периодические и бесконечно дифференцируемые в области определения, но не непрерывные. Тангенс и секанс имеют разрывы второго рода в точках 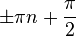 , а котангенс и косеканс — в точках
, а котангенс и косеканс — в точках 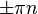 .
.
 2015-04-06
2015-04-06 13206
13206
